Before we begin our discussion on Motion in two dimensions (2D), let us answer these 3 questions.

(If you need an Online Physics Tutor to explain these concepts in a private 1:1 mode, feel free and get started immediately on WhatsApp !)

What is motion in 2 dimensions (2D)?

The motion of a particle in a plane is called 2-dimensional motion.

Example: An insect crawling on your laptop or mobile screen but not flying above it.

Can there be motion in 2 dimensions (2D)?

Yes! Motion in two dimensions is possible. It is pretty common to have 2-dimensional motion.

Some examples of 2D motion are Projectile motion, Circular motion, motion in a plane (planar motion), etc.

How do we tackle the motion in 2D?

Break the motion into two separate components, x, and y, and treat each component as a separate motion. But since it is a motion of a single object so, at one time, the body can only be in one place. Using this constraint, we can correlate the two separate equations and solve them for unknowns.

Why does this strategy work?

The concept of motion, when a particle moves along a straight line, can be used for motion in a plane. When the motion of a particle is in-plane, we generally consider the plane of motion as the x-y plane. We choose the origin at the place from where the motion starts, and then we consider motion along any two convenient mutually perpendicular directions as one-dimensional motion. Motion in two perpendicular directions is chosen as the x and y-axes.

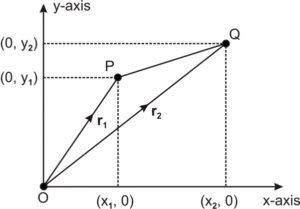
Position

Suppose a particle moves in a plane along the curve as shown in figure. At time {t_1}  the particle is at point P and at some later time {t_2}, the particle is at Q. As the particle moves from P to Q in the time interval \Delta t = {t_2} - {t_1},

the position vector changes from {{\bf{r}}_1} to {{\bf{r}}_2}

from the triangle rule of vector addition, we can write

{\bf{OP}} + {\bf{PQ}} = {\bf{OQ}}\quad \Rightarrow \quad {\bf{PQ}} = {\bf{OQ}} - {\bf{OP}}\quad \Rightarrow \quad {\bf{PQ}} = {{\bf{r}}_2} - {{\bf{r}}_1}

{\bf{\Delta r}} = {{\bf{r}}_2} - {{\bf{r}}_1}

Here, {{\bf{r}}_1} = {x_1}\hat i + {y_1}\hat j and {{\bf{r}}_2} = {x_2}\hat i + {y_2}\hat j

{{\bf{r}}_2} - {{\bf{r}}_1} = ({x_2} - {x_1})\hat i + ({y_2} - {y_1})\hat j = \Delta x\hat i + \Delta y\hat j

\Delta {\bf{r}} = \Delta x\hat i + \Delta y\hat j; where \Delta x = ({x_2} - {x_1}) and \Delta y = ({y_2} - {y_1})

 

So we see here that motion in an x-y plane can be simplified into two separate motions; one in the x-direction and one in the y-direction. Hence the strategy that we discussed to tackle the 2D motion works.

Velocity

We define the particle’s average velocity during the time interval \Delta t as the ratios of the displacement of that time interval.

{{\bf{v}}_{av}} = \frac{{{\bf{\Delta r}}}}{{\Delta t}} = \frac{{\Delta x\,\hat i + \Delta y\,\hat j}}{{\Delta t}}

{{\bf{v}}_{av}} = \frac{{{\bf{\Delta r}}}}{{\Delta t}} = \frac{{\Delta x\,\hat i}}{{\Delta t}} + \frac{{\Delta y\,\hat j}}{{\Delta t}}

\mathop {\lim }\limits_{\Delta t \to 0} \frac{{{\bf{\Delta r}}}}{{\Delta t}} = \mathop {\lim }\limits_{\Delta t \to 0} \left( {\frac{{\Delta x}}{{\Delta t}}} \right)\hat i + \mathop {\lim }\limits_{\Delta t \to 0} \left( {\frac{{\Delta y}}{{\Delta t}}} \right)\hat j

{{\bf{v}}_{inst.}} = {v_x}\hat i + {v_y}\hat j

{{\bf{v}}_{inst.}} is instantaneous velocity.

Acceleration

The average acceleration of a particle as it moves from P to Q is defined as the ratio of the change in the instantaneous velocity vector

{{\bf{a}}_{av}} = \frac{{{\bf{\Delta v}}}}{{\Delta t}}

and {{\bf{a}}_{{\rm{inst}}{\rm{.}}}} = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{{\bf{\Delta v}}}}{{\Delta t}} = \frac{{d{\bf{v}}}}{{dt}}

{{\bf{a}}_{{\rm{inst}}{\rm{.}}}} = \frac{d}{{dt}}\left( {{v_x}\hat i + {v_y}\hat j} \right) = \frac{{d{v_x}}}{{dt}}\hat i + \frac{{d{v_y}}}{{dt}}\hat j

{{\bf{a}}_{{\rm{inst}}{\rm{.}}}} = {\bf{a}} = {a_x}\hat i + {a_y}\hat j

Because {\bf{a}} is normally assumed as constant, its component {{\bf{a}}_x} and {{\bf{a}}_y} are also constants. Therefore we can apply the kinematics equations to the x and y components of the velocity vector and displacement vector as follows.

{\bf{V}} = {{\bf{V}}_0} + {\bf{a}}t\left\{ {\begin{array}{*{20}{c}} {{v_x} = {{({v_x})}_0} + {a_x}t}\\ {{v_y} = {{({v_y})}_0} + {a_y}t} \end{array}} \right.

{\bf{r}} = {{\bf{V}}_0} + \frac{1}{2}{\bf{a}}{t^2}\left\{ {\begin{array}{*{20}{c}} {x = {{({v_x})}_0}t + \frac{1}{2}{a_x}{t^2}}\\ {y = {{({v_y})}_0}t + \frac{1}{2}{a_y}{t^2}} \end{array}} \right.

{v^2} = u_0^2 + 2as\left\{ {\begin{array}{*{20}{c}} {v_x^2 = ({v_x})_0^2 + 2{a_x}{s_x}}\\ {v_y^2 = ({v_y})_0^2 + 2{a_y}{s_y}} \end{array}} \right.

In other words, two-dimensional motion with constant acceleration is equivalent to two independent motions in the x and y directions having constant accelerations {a_x} and {a_y}.

Examples of two-dimensional motion

Projectile motion

When an object is thrown at some angle to the horizontal, the projectile’s motion will be in the horizontal and vertical directions. Suppose the motion of the projectile is in the x-y plane of the coordinate system. The object’s motion will be along two mutually perpendicular directions together, say the x and y axes of the coordinate system. Consider motion along the horizontal direction (x-axis) and motion along the vertical direction (y-axis).

\begin{array}{*{20}{c}} {{v_x} = u\cos \theta }\\ {x = x}\\ {{a_x} = 0} \end{array}

\begin{array}{*{20}{c}} {{v_y} = u\sin \theta }\\ {y = y}\\ {{a_y} = - g} \end{array}

So, the equation of kinematics for one-dimensional motion can be used.

Watch this video on 2D motion, precisely projectile motion, to better understand the concept.

Circular motion

Circular motion is a type of motion in a plane in which a particle moves around a fixed point such that its distance from a fixed point is constant.

Suppose a particle moves on a circular path uniformly, as shown in the figure.

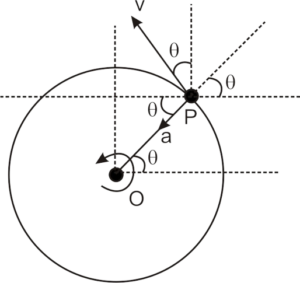
Here, R is the distance from the fixed point, the center of this circle, to the particle.

{\bf{R}} = R\cos \theta \hat i + R\sin \theta \hat j

x = R\cos \theta \,;\,\,y = R\sin \theta

{\bf{v}} = - v\sin \theta \hat i + v\cos \theta \hat j

{v_x} = ( - v\sin \theta )\,;\,\,{v_y} = (v\cos \theta )

{\bf{a}} = a\cos \theta ( - \hat i) + a\sin \theta ( - \hat j)

{a_x} = - a\cos \theta

{a_y} = - a\sin \theta

Click the link for an in-depth guide on circular motion.

Watch this video about

Solved problems on two-dimensional motion

Example 1

A helicopter on a flood relief mission flying horizontally with speed u at an altitude H has to drop a food packet for a victim standing on the ground. At what distance from the victim should the packet be dropped? The victim stands in the vertical plane of the helicopter’s motion.

Solution

We can solve this problem by using the concept involved in motion in a plane.

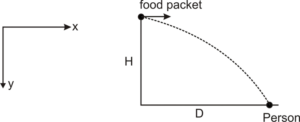
Suppose the velocity of the food packet at the time of release is v and is horizontal. The vertical velocity at the time of release is zero.

The motion of the food packet along the y-axis.

y = {u_y} + \frac{1}{2}{a_y}{t^2}

Here, y = H\,;\,\,{u_y} = 0\,;\,\,{a_y} = g

H = 0 + \frac{1}{2}g{t^2}\quad \Rightarrow \quad t = \sqrt {\frac{{2H}}{g}}

Again, the motion of the food packet along the x-axis,

x = {u_x}t + \frac{1}{2}{a_x}{t^2}

Here, let x = D\,;\,\,{u_x} = u\,;\,\,{a_x} = 0

\Rightarrow \quad D = ut + 0\quad \Rightarrow \quad D = ut

    D = u\sqrt {\frac{{2H}}{g}}.

Therefore, the required distance equal to D = u\sqrt {\frac{{2H}}{g}}.

Example 2

A projectile is given an initial velocity of (\hat i + 2\hat j) m/s where \hat i is along the ground and \hat j is along the vertical of g = 10\,{\rm{m/}}{{\rm{s}}^{\rm{2}}} then find equation of trajectory.

Solution

This problem is based on the concept of motion in a plane.

We can study the two-dimensional motion as one-dimensional along the x-axis and y-axis since its superposition gives the resultant motion.

{({v_x})_i} = 1\,{\rm{m/s}}\,{\rm{;}}\,\,{{\rm{a}}_x} = 0

{({v_y})_i} = 2\,{\rm{m/s}}\,{\rm{;}}\,\,{{\rm{a}}_y} = - 10\,{\rm{m/}}{{\rm{s}}^2}

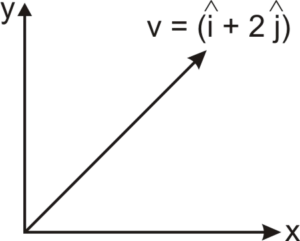
Using motion of the projectile along x-axis,

x = {u_x}t + \frac{1}{2}{a_x}{t^2}

So, x = 1 \times t + \frac{1}{2} \times (0){t^2}

x = t            …(i)

Again, using motion of the projectile along y-axis,

y = {u_y}t + \frac{1}{2}{a_y}{t^2}

y = 2 \times t + \frac{1}{2} \times ( - 10){t^2}

So, y = 2t - 5{t^2}

Putting the value of t = x in the above equation

y = 2x - 5{x^2}

This is the required equation of trajectory.

Example 3

The particle has initial velocity (3\hat i + 4\hat j) and an acceleration of (0.4\hat i + 0.3\hat j). Find speed of particle after 10 sec.

Solution

Here, in this question, it is given that

({u_x}) = 3\,unit\,;\,\,{a_x} = 0.4\,unit

({u_y}) = 4\,unit\,;\,\,{a_4} = 0.3\,unit

Since the acceleration of the particle is constant so, we can use

{({v_x})_f} = {({v_x})_i} + {a_x}t and {({v_y})_f} = {({v_y})_i} + {a_y}t

{({v_x})_f} = 3 + (0.4 \times 10) and {({v_y})_f} = 4 + (0.3 \times 10)

So, {({v_x})_f} = 3 + 4 and {({v_y})_f} = 4 + 3

{({v_x})_f} = 7\,unit  and {({v_y})_f} = 7\,unit

Now, we can write

{{\bf{v}}_f} = {({v_x})_f}\hat i + {({v_y})_f}\hat j

{{\bf{v}}_f} = (7\,unit)\hat i + (7\,unit)\hat j

Speed of particle = \left| {{{\bf{v}}_f}} \right|

= \sqrt {{{(7\,unit)}^2} + {{(7\,unit)}^2}}

= (7\,unit)\sqrt 2 = 7\sqrt 2 \,\,unit

Example 4

A particle moves in x-y plane under the action of a force {\bf{F}} such that the value of its linear momentum {\bf{P}} at any time t is {P_x} = 2\cos t\,;\,\,{P_y} = 2\sin t. Find the angle \theta between {\bf{F}} and {\bf{P}} at a given time t.

Solution

Here momentum vector of the particle can be written as

{\bf{P}} = {P_x}\hat i + {P_y}\hat j

{\bf{P}} = 2\cos t\,\hat i + 2\sin t\,\hat j

Now, from Newton’s 2nd law of motion;

We can obtain force as {\bf{F}} = \frac{{d{\bf{P}}}}{{dt}}\quad \Rightarrow \quad {\bf{F}} = \frac{d}{{dt}}\left( {2\cos t\,\hat i + 2\sin t\,\hat j} \right)

{\bf{F}} = \frac{{d{\bf{P}}}}{{dt}}\quad \Rightarrow \quad {\bf{F}} = \frac{d}{{dt}}\left( {2\cos t\,\hat i + 2\sin t\,\hat j} \right)

Now, using scalar product of two vector for calculation angle between {\bf{F}} & {\bf{P}}.

{\bf{P}} \cdot {\bf{F}} = \left| {\bf{P}} \right|\left| {\bf{F}} \right|\,\cos \theta

\cos \theta = \frac{{{\bf{P}} \cdot {\bf{F}}}}{{\left| {\bf{P}} \right|\left| {\bf{F}} \right|}} = \frac{{(2\cos t\,\hat i + 2\sin t\,\hat j) \cdot ( - 2\sin t\,\hat i + 2\cos t\,\hat j)}}{{\left| {\bf{P}} \right|\left| {\bf{F}} \right|}}

\cos \theta = \frac{{ - \,4\sin t \cdot \cos t + 4\sin t \cdot \cos t}}{{\sqrt {{{(2\cos t)}^2} + {{(2\sin t)}^2}} \sqrt {{{( - 2\sin t)}^2} + {{(2\cos t)}^2}} }}

\cos \theta = 0\quad \Rightarrow \quad \theta = 90

So, the angle between the force vector and momentum vector is 90º.

 

Author
  • Rajesh Kumar

    20 years of experience teaching high school and college physics to students across the globe.

    When not teaching or mentoring, I write informative articles in physics and related subjects. So far, I have written more than 200 articles on different topics in physics. Apart from physics, I am proficient in engineering statics, dynamics, and calculus. I love spending time with my kids and listening to old Hindi songs.

    Recent Posts
    The Law of Conservation of Angular Momentum
    Angular Momentum
    Torque