Physics of Projectile Motion

When we throw an object high up in the air, the object is called a projectile, and the path it follows is called its trajectory. Once the object is released, it no longer experiences the initial force but comes under the influence of gravity and the air drag (or friction). However, in this article, we will ignore the effects of air resistance to keep things simple. A few simple examples of projectile motion are throwing a stone (at some angle from the horizon or straight overhead), dropping a stone into a ditch, launching a satellite into Earth orbit, or sending interplanetary probes.

My Engineering Buddy provides the #1 online physics tutoring service on the web. In case you need one, feel free to WhatsApp us.

Equations of motion

Before we proceed further, we assume that you are familiar with the three equations of motion, namely,

$v = u + f\times t \hspace {30}-----[A]$

$s= ut + \frac {1}{2}ft^2 \hspace {30} -----[B]$

$v^2 = u^2 + 2fs \hspace {30} ----- [C],$

where $u$ is the initial velocity, $v$ is the final velocity, $f$ is the acceleration, and $t$ is the flight time.

Physics of projectile motion

Let us draw a diagram to understand the physics of the projectile motion. Assume the object’s initial velocity is $v$ , and it is projected at an angle from the horizon. Also, assume that it attains a maximum height of $h$ and then starts falling down and finally touches the ground at point R units away from the throwing point.

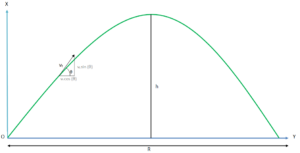
Figure 1. The motion of an object thrown up from the ground at an angle.

The velocity of the particle $t$ seconds after its projection is labeled as $v_t$ . It is directed at $\theta_t$ degrees from the horizon. It has $v_t \cos\theta_t$ and $v_t\sin\theta_t$ as the horizontal and vertical components.

Let us say at $t = 0$ , $v_0 = u$ . Further, let the initial projection direction to the ground (horizon) be represented as $\theta_0$ for simplicity. We label it as $\theta$ . We divide the initial velocity into horizontal and vertical components, $u\cos\theta$ and $u\sin\theta$ . The projected object experiences only one force on it, the gravitational pull downwards, which produces acceleration $g$ that is acting against the vertical component of projection velocity and hence decelerates the object until its vertical velocity becomes $0$ . At that point, the object attains height $h$ above the horizon and starts falling. However, all the while, the horizontal component of the velocity finds no resistance (as gravity is acting at a right angle to it, we have ignored any effects of air resistance in our calculation). Let $T_1$ be the time the object takes to reach the maximum height $h$ .

Following the formula [A], $Final \hspace {3} Velocity = Initial \hspace {3}Velocity - Acceleration \times Time$ .

$0= u\hspace {2}\sin\theta - g\times \hspace {3} T_1$

$\therefore T_1 = \frac {u\hspace {2}\sin\theta}{g} \hspace {60}-----[1]$

Using formula [C], we write,

$0^2 = (u\hspace {2}\sin\theta)^2 - 2 \times g \times h$

hence, $h = \frac{(u\hspace {2}\sin\theta)^2}{2g} \hspace {30}-----[2]$

Nature of projectile’s flight path

This was the calculation for the part the object was traveling up. For the descent, the initial velocity’s vertical component is zero, there is acceleration $g$ which is now bringing it down, the horizontal component is undisturbed with value $u\cos\theta$ and another known quantity is the distance to be traveled before the object touches ground $h$ . Let $T_2$ be the time the object takes to fall from the top point while traversing the distance to the ground $h$ . Now, using the equation [B],

$h=0\times T_2 + \frac{1}{2}gT_2^2 = \frac{1}{2}gT_2^2 \hspace{7} -----[3]$

Equating the value of $h$ from [2] and [3],

$\frac{(u\hspace {2}\sin\theta)^2}{2g} = \frac{1}{2}gT_2^2$

$\therefore T_2 = \frac {u\hspace {2}\sin\theta}{g}$ , which is the same as $T_1$ (confer with [1]).

We have, therefore, proved that the flight path or trajectory is symmetrical in time on both the sides of maximum height. This means the trajectory is a curve which is symmetrical on both the sides of the vertical line of height $h$ . We can therefore write the equation for total time $T$ of the flight,

$T = T_1 + T_2 = \frac {2 \hspace {2} u\sin\theta}{g} \hspace {30} -----[4]$

The horizontal range of the projectile $R$ is the horizontal velocity multiplied by total time $T$ .

$R = u\cos\theta \times \frac {2 \hspace {2} u\sin\theta}{g}$

$R = \frac {u^2} {g} \times (2 \hspace {2}\sin\theta \hspace {2} \cos\theta)$

$R = \frac {u^2 \sin 2\theta}{g} \hspace {75} -----[5]$

We know that $\sin 90^{\circ} = 1$ ; from relation [5] above we conclude that the maximum range would be attained by the projectile if it is thrown at an angle of $45^{\circ}$ from the horizon.

>Copying formula [3] here and putting the value of $T$ from [4],

$h= = \frac{1}{2}g(\frac {u\sin\theta}{g})^2$

$\therefore h= \frac {u^2{(\sin\theta})^2}{2g} \hspace{60} -----[6]$

What is the position of the object at time $t$ after the launch? It is equal to the the velocity multiplied by time in case of uniform speed and in case of acceleration it is given by equation of motion [B].

$x = u \times \cos \theta \times t \hspace{0.75 in} -----[7]$

or, $t = \frac {x} {u \cos \theta} \hspace{1 in} -----[7A]$

$y = u \sin\theta \times t - \frac{1}{2} \times g \times t^2 \hspace{10} -----[8]$

Upon putting the value of $t$ from [7A] into [8] we get,

$y = x \tan \theta - \frac{1}{2}g \left( \frac{x}{u {\cos\theta}} \right)^2$

$y = \tan \theta \times x - \frac{g} {2 {(u \cos \theta)^2}} \times x^2 \hspace {1} -----[9]$

which is of the form,

$y = Ax^2 + Bx + C \hspace {40} -----[10]$

– the standard equation of a parabola.

Let us give $\theta$ some numerical value, say, $45^{\circ}$ , then in [8] we have $\tan 45^{\circ} = 1$ , and $\cos 45^{\circ} = \sin 45^{\circ} = \frac {1}{\sqrt 2}$ and for simplicity’s sake, we further assume $g=1$ (instead of 0.98) and $u = 1 m/s$ . The equation [9] becomes,

$y = x - x^2$

When we trace it, it clearly shows that it is a parabola. Please give some other values to $\theta$ and experiment.

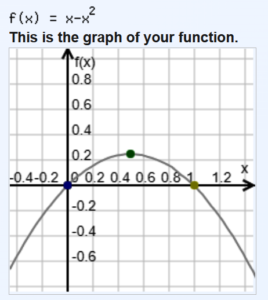[Figure 2: Plotted using Mathpower]

However, a projectile need not be thrown up from and land on the ground (the zeroth item in the list below). There can be other situations.

Different situations

0. An object is thrown up from the ground at an angle.
1. An object is dropped from a height.
2. An object is thrown straight overhead.
3. An object is thrown horizontally from a height.
4. An object is thrown at such a speed and angle that it starts circumnavigating the Earth.

An object is dropped from a height.

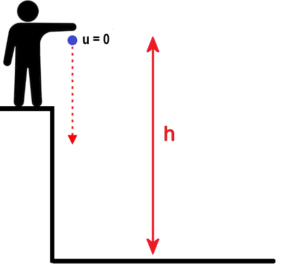
Figure 3. An object is dropped from a height.

Here $u = 0$ , $\theta = 0$ , and acceleration is $g$ ; from equation [B] we get,

S= h = $0 \times\ t + \frac{1} {2} g t^2$

So, the time $t$ to fall to the ground is $\sqrt \frac{2 h} {g}$ .

The speed with which the object hits the ground is given by the formula [C] and is $v =\sqrt {2gh}$ .

What if the object is thrown vertically upwards with speed u and reaches height h?

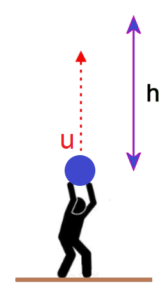
Figure 4. An object is thrown straight overhead.

The object slows down when its speed $v = 0$ , hence equation [C] becomes, $0^2 = u^2 - 2 gh$ , we get the maximum height reached, $h=\frac{u^2}{2g}$ and the time taken in doing so from relation [A], $0 = u - gt$ ( $u$ and $g$ are directed oppositely), we get $t = \frac{u}{g}$ and the total time from throwing up to falling back to the launch height $t = \frac{2u}{g}$ .

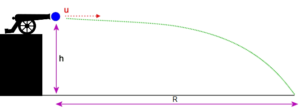
Figure 5. An object is thrown horizontally from a height.

In this case the initial velocity is horizontal, hence the vertical component is 0. The time the object will take to fall to ground from the height h can be found by formula [B].

$h&=0 \times t + \frac {1} {2} \times g \times t^2$

$t &= \sqrt \frac {2h} {g}$

And the range R is again given by equation [B], but here we put the initial velocity horizontal component u in the equation, and there is no acceleration involved in the horizontal direction; or, simply put, Distance = speed x time.

R= ut = u $\sqrt \frac {2h} {g}$

Launching of satellite and space missions, Computation of orbital velocity

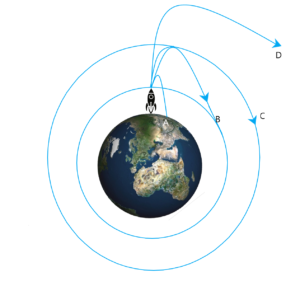
Figure 6: The picture above shows 4 situations, A, B, C, and D.

In case A the launch velocity is small, and the object or rocket, after reaching its maximum height, falls toward the ground and lands at a place away from the launch site.

If the object’s velocity is higher, it will fall further and further away from the launch point.

In cases B and C, the launch velocity is so high that it eventually covers the same distance horizontally that the Earth’s curvature causes the ground to fall away vertically. The object is said to be in orbit. The higher velocity in case C pushes it to a higher orbit. The following formula gives the orbital velocity of the satellite,

$v=\sqrt \frac {GM} {r}$ ,

where $M$ is the mass of the larger body (in this case, Earth’s mass), $r$ is the distance from the center of the Earth, and $G$ is the gravitational constant = 6.67430 × 10^-11m³kg^-1s^-2.

Derivation: In our discussion on the circular motion, we observed that the centripetal acceleration of a body is given by the formula $\frac{v^2}{r}$ . From Newton’s law of gravitation, we know that the gravitational force of attraction between two bodies having masses $m$ and $M$ and having the separation $r$ is given by the formula:

$F = \frac{GMm}{r^2}$ .

However, we are more familiar with $F = mg$ (on the surface of the Earth), so we can write $g = \frac{GM}{r^2}$ ; however, we should observe caution that g=9.8 m/s² is the value on the surface of the Earth where $r$ = radius of the Earth. For a rocket launch, we must use the formula $F =\frac{GMm}{r^2}$ as the object is much above the Earth’s surface, so the acceleration due to gravity is lesser.

Hence the acceleration on mass $m$ is $a = Force /m$ .

Thus, $\frac {v^2}{r}= \frac{GM}{r^2}$ , or $v = \sqrt \frac{Gm}{r}$ .

In a Low Earth Orbit (LEO), the velocity comes to approximately 25,000 km/h, which is 6.94 km/s. Any rocket will burn up soon after the launch at this speed due to air friction.

Therefore, in actual practice, rockets are made of several stages, say 3 to 5, every higher stage lighter than the previous one. Each stage falls off after imparting some boost, as the rocket has become lighter after detachment of the previous stage and the ignition of the next; it can achieve higher speed as it has sufficiently moved up from the hazard of burning up in the atmosphere.

Now we come to the exciting situation depicted in the above figure as D. Here, the launch velocity is so high that the object neither falls back on Earth nor revolves around it in some orbit but instead frees itself from the trappings of the Earth’s gravity never to come back. Such a launch speed is called the escape velocity. It can be calculated easily by equating the potential energy of the object and its kinetic energy.

An object at a height h (from the surface of the Earth) has the potential energy $mgh$ with respect to the surface of Earth and $mgr$ with respect to the center of the Earth; its kinetic energy is given by the formula $\frac{1}{2} mv^2$ . Upon equating the two energies we get, $v = \sqrt {2gr}$ . The term $g$ is specifically used for Earth so we substitute it by $\frac {GM} {r^2}$ and we get $v_{escape} = \sqrt \frac {2GM}{r}$ .

When substituting the G, M, and Earth’s radius values, we get a value of 11.2 km/s. This is the value of escape velocity at the surface of the Earth. However, in actual practice, as explained earlier, objects are never launched at such a monstrous speed to obviate frictional burning.

We notice that the value of escape velocity does not depend upon the mass of the projected body. Instead, it depends on the mass and radius of the planet from which it is projected. The value of escape velocity does not depend on the angle and direction of the projection.

Geostationary (Geosynchronous) Satellites

The objects that move around the earth are said to be in geocentric orbits, such as the Moon and artificial satellites.

Figure 7: Geosynchronous orbit animation (courtesy Wikipedia). This demonstrates a satellite in a geosynchronous orbit (not to the scale) around the Earth. The period of the satellite is the same as the period of Earth’s rotation, one day. If the satellite is established in orbit in the equatorial plane, it appears stationary above a station; hence, such orbit is also called the geostationary orbit. Communication satellites are usually put in such orbits.

A circular geosynchronous orbit has a constant altitude (height from Earth’s surface) of ~ 35,786 km, and the orbital speed is ~ 11,300 km/h (about 3 km/s).

Some numerical examples.

1. An object is projected from the ground at an angle of 30⁰ with an initial speed of 10 m/s; calculate the time of flight, horizontal range, maximum height, and equation of motion. Take $g$ = 10 m/s².

We have, $\sin 30^{\circ}= 1/2, u = 10, g = 10$ , we invoke our derived equation [4] above and substitute values,

$T = 2 \times \frac {u \sin\theta} {g} = 2 \times \frac {10 \times \frac {1}{2}} {10} = 1 s$

Invoking equation [5] and putting values,

$R = u^2 \frac {\sin 2\theta} {g} = 10^2 \times \frac {\frac {\sqrt 3}{2}} {10} = 5\sqrt 3 \hspace {3}or \hspace {3}8.66 \hspace {3}m$ .

Let us now evaluate the height; we get back to the formula [6] and substitute numerical values,

$h= \frac {u^2{(\sin\theta})^2}{2g} = \frac {10^2 \times (1/2)^2}{2\times 10} = 25/20 \hspace{3} or, \hspace{3}1.25 m$

We recall the equation of the path of the projectile given in [9] and put the numerical values,

$y = \tan \theta \times x - \frac{g} {2 {(u \cos \theta)^2}} \times x^2$ , and we get,

$y &= (1/\sqrt 3) x - [(1/2) \times 10 ) / (10 \times \sqrt 3/2)]^2\times x^2$

$y = 0.57735 \times x - (5 * 5*1.732)^2 \times x^2$

$y = 0.57735 \times x - 43.3013 \times x^2$ , which is the equation of a parabola.

2. A ball is thrown at an angle 30⁰ with initial speed 20 ms^-1, g = 10 ms^-2. There is 3 m high wall at 10 m from the projection point. Find out whether the ball will strike the wall or go to the other side.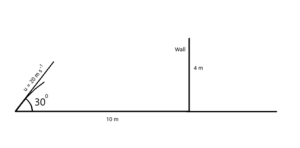Figure 8: Will the projectile hit the wall or fall to the other side?

Here the relevant quest is the height, but we shall also find the range to see if something interesting will happen. Using the equations of the first example, we get the maximum height as 5 m and the range as 34.64 m. So the ball will not hit the wall but will land 34.64 m away from the launching point. Since the maximum height of the projectile is more than the wall height, it will not hit the wall and continue to travel and hit the ground 34.64 m away.

3. Using the values given in example (2) above, find out what time(s) the projectile will be 3 m above the ground.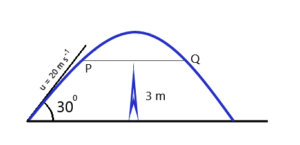

Figure 9: With the given values, find out the time(s) taken by the projectile to achieve 3 m vertical height from the ground.

Using equation [B], namely, $s= ut + \frac {1}{2}ft^2$ , we put $s$ =3, $u = 20 \times \sin 30^{\circ}$ , and $g$ = -10, we get,

$3 = 20 \times (1/2) \times t - (1/2) \times 10 \times t^2$

or, $5t^2 - 10t + 3 = 0$ which when solved for $t$ gives us 0.37 s and 1.63 s as the answers which correspond to the points P and Q in the figure 9.

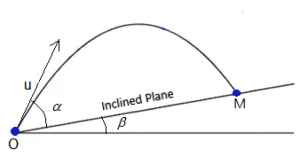
Figure 10.

Example 4. In the figure above, a projectile is launched from point O at an angle of $\alpha$ = 25° a plane inclined at $\beta$ = 15° to the horizon. The initial velocity u is 20 m/s. The projectile hits the inclined plane at point M.

Find the time it takes for the projectile to hit the inclined plane at M and the distance OM.

On the inclined plane it is obvious that $x, y$ coordinates of point M are related by $\frac{y}{x} = \tan\beta$ . Let the launch angle with respect to the horizon be $\theta \hspace {3} (= \alpha + \beta) = 40^0$ .

$OM$ can be calculated later using the relation, $OM= x \times \sec \beta$ , moreover the $x, y$ components of the position of the projectile are given by,

$x = u \times\cos \theta \times t$ , $y = u \times \sin \theta \times t - (1/2) g \times t^2$ .

We shall use the the equation of motion [B] to find the x and y components of the distance travelled. $S = u\times t - \frac {1}{2} g\times t^2$ .

$x = u \cos \theta \times t \hspace {70} -----[Q]$

and

$y= u \sin \theta \times t - \frac {1}{2} g\times t^2 \hspace {30} -----[R]$

Substituting the values of $x$ and $y$ from equations [Q] and [R] in the the relation $\frac{y}{x} = \tan\beta$ we can write,

$\tan\beta = \frac {u \sin \theta \times t - [\frac {1}{2}] g\times t^2} {u \cos \theta \times t}$ .

Taking $t$ common on the RHS ( $t$ = 0 as the trivial solution which only tells that the object was on the ramp at point $O$ at the time of launch. Further, upon putting the numerical values of $\beta$ , $u$ and $\theta$ , the equation becomes,

$0.26795 = \frac {20 \times 0.64279 - \frac {1}{2} 9.8\times t} {20 \times 0.76604}$

Thus, $4.9\times t &= 20\times 0.64279 - 20\times 0.76604 \times 0.26795$

$t &= 1.8 \hspace {3}s$

The $x$ coordinate of point $M$ is given by

$x = u \cos \theta \times t$

Putting the numerical values of $\theta$ and $t$ ,

$x = 20 \times 0.766044 \times t$

$x = 15.32 \hspace {3}m$

Since, $OM= x \times \sec \beta$ , thus, $OM =15 \times 1.10338$ .

$\therefore OM= 16.55 \hspace {3}m$

Resources:

Projectile Motion Calculators:

Several Projectile Motion Calculators are available on the net, some do specific calculations such as range or height, but others are more versatile, such as the following two.

Omni Calculator and Projectile Motion Calculator by Physics Catalyst.

I found the latter particularly useful. Here is a snapshot:

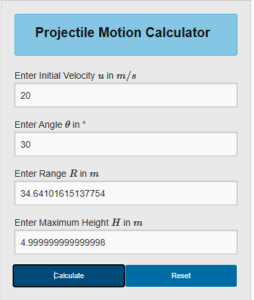
In the above fields, we are required to put any two inputs; if we put more, the calculator prompts, “you have entered more than 2 values. Please leave two text boxes empty. Other two text boxes will be calculated based on that”. In the above snapshot, I had put the initial velocity as 20 m/s and the angle as 30⁰. Upon pressing the “Calculate” button, the answer was “Range = 34.64 m and height 5 m”.

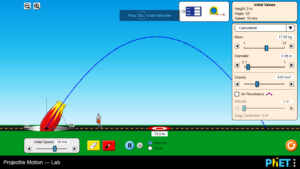
The University of Colorado interactive Projectile Motion Simulator.

It is part of their PhET website, originally an acronym for “Physics Education Technology.” This page covers several other topics in physics as well. Here one can interactively change the speed and inclination of the cannon, and upon pressing the “fire” button, the cannonball traces a parabolic trajectory. The flight parameters appear in a pane on the right. Here is a snapshot. You may notice that at the bottom of the right pane, one can also study the effects of air resistance. With a drag coefficient of 0.47, it calculates the drag depending upon the object’s velocity and altitude (air gets thinner as we go up, which especially applies to rockets and missiles).

Some other sites:

Projectile Motion Lab, Virtual Amrita Laboratories, Khan Academy Videos on this topic, and many more. All these, in their ways, deal with the subject, calculate parameters and display the projectile path.

Author

Rajesh Kumar

20 years of experience teaching high school and college physics to students across the globe.

When not teaching or mentoring, I write informative articles in physics and related subjects. So far, I have written more than 200 articles on different topics in physics. Apart from physics, I am proficient in engineering statics, dynamics, and calculus. I love spending time with my kids and listening to old Hindi songs.

Recent Posts

The Law of Conservation of Angular Momentum

Angular Momentum

Torque