On the Significance of Significant Figures
In Mathematics, we do our calculations using some numbers, and the result is another number. In Physics, Chemistry, Engineering Sciences, or even Biological Sciences, we take measurements, do calculations and end up with some results. Most of the time, these results are some numbers. Sometimes these numbers are small, sometimes massive, and sometimes have some fractional part represented by a string of numbers after the decimal point. We often encounter a problem here ‘to how many decimal places should I report the answer?’ It is precisely where the concept of ‘significant figures‘ comes into play.
If you wish to recapitulate your number system knowledge, you may click this link.
Significant figure example: the number π (pi)
A good example of significant figures is the natural number π (pi). As we all know, it is the ratio of the circumference of a circle to its diameter. No matter how big or small you draw a circle; this ratio is always the same, a natural constant. For thousands of years, humankind has tried to evaluate this constant precisely. It is a transcendental number, and we cannot calculate it using an equation involving only sums, products, powers, and integers. It is an irrational number; thus, we cannot represent it as a ratio of two integers. Its earliest value for most applications is the approximation 22/7, a rational number, and it gives the value of π correct to only 2 decimal places, 3.14.
Better approximation of π (pi)
A better approximation is 355/113; it gives a correct value down to the decimal’s sixth place as 3.141592. A better one is 104348/33215, which correctly approximates up to 9 decimal places, 3.141592653. Using modern computers, the value π has been evaluated accurately to millions of places after the decimal. On 14 August 2021, a team at the University of Applied Sciences of the Grisons in Switzerland announced their completion of the computation of π to 62.8 trillion digits. Mind-boggling and useless for us for any practical purpose! The question is, how precise a value π do we require? For most practical applications in science, a value of π = 3.14159, up to only 5 decimal places, is sufficient.
Imagine you have a cemented circular platform in your garden and wish to enhance its appearance with porcelain tiles. You take a tape measure and find that its diameter is 4 meters (that is as accurate as you can measure with a tape measure), meaning it has a radius of 2 meters. The question is how many tiles would be required to cover the platform. The tiles supplied by the manufacturer are squares of 12 inches by 12 inches (it says so, on the packing box). It is a case of simple arithmetic; the area of the circular platform is (π r2) = π x 2 x 2 = 4 π m2. The area of the tiles is 12 x 12 or 144 inch2. We have to bring them to the same units before we take the next step of dividing the platform area by tile area.
Let us settle for centimeters, so the circle area is 40,000 x π sq cm. Now, 144 sq inch = 144 x 2.54 x 2.54 sq cm. Dividing 40,000 x π by 144 x 2.54 x 2.54 (= 929.0304) we get 43.055642 x π tiles. We take the value of π as 3.14159; the answer is 135.26317 tiles; since the number of tiles should be a round number, we round off the answer to 135 tiles. Even if we had taken the value of p only to 2 decimal places, that is, 3.14, the answer would still be the same, 135 tiles. The preceding raises the important question of ‘significant figures’ in maths and science. What is the count of digits that is reliable and necessary to represent the true value of a number?
Having sown some questions about the desired or significant number of decimal places in your minds, we now break away from this example and move straight to what is meant by significant figures in Mathematics. The basic idea behind significant figures is to do away with false precision.
Rules for Significant Figures
All non-zero digits of a number are significant.
The number 24357 contains 5 digits. And all the 5 are significant.
All leading zeroes of a number are insignificant.
If someone reports that the length of a pole is 017 feet, he means it is 17 feet, the leading zero is insignificant, and there are just 2 significant digits in the number 017.
Trailing zeroes of a number are insignificant.
Thus 2500 has only two significant digits, 2 and 5.
What if zeroes occur between non-zero digits of a number?
Well, then they are all significant. For example, 24030507 is an 8-digit number, and all the 8, including the three zeroes, are significant – necessary to represent the value of the number.
The story gets a twist when the decimal point comes in.
Take the above example of 2500; if we had written it as ‘2500, ‘ all the 4 digits would have been significant. Why? The decimal indicates that the measurement was precise enough to go to the fractional level, but the result was a whole number without anything after the decimal.
We consider zero insignificant if a decimal number has the whole part as zero. For example, in 0.1, there is only 1 significant digit, and likewise, in 0.25, there are 2 significant digits, 2 and 5.
It may seem very peculiar, but 0.025 also has only 2 significant digits by definition. The rule is that the zeros on the right of the decimal point and to the left of a non-zero digit are insignificant. Thus, 0.00645 has only three significant digits. What are the implications, and why is it so? Imagine you are measuring the length of a short, newly constructed patch of road. Your surveyor reports its length as 0.0486 km, which is the same as 48.6 meters. Thus, only 3 digits are significant, 4, 8, and 6.
However, if the reported result was 0.04860 km, the number of significant digits becomes 4, and the last zero is significant. Why? The rule is that all zeros on the right of a decimal point are significant only if a non-zero digit does not follow them. For example, 20.00 contains four significant digits. In our example, it means the length of the patch of road is 48.60 meters, the person was trying to measure it correctly down to the last centimeter, but that last centimeter turned out to be zero.
Significant places are all about measurements, methods, and inherent and desired precision. Some other examples: 0.0064500 contains 5 significant digits, including the trailing zeroes. Since 2070 m means it is the result of a measurement, the trailing 0 is significant, and thus the number has 4 significant digits.
More examples of significant figures
(the digits in bold are significant figures)
6500 {2}
6005 {4}
6500. {4}
6050.60 {6}
As a general rule, significant figures of a number are any non-zero digits or trapped zeros, and they do not include leading or trailing zeros.
Significant figures in multiplication or division
The final answer in a multiplication or division problem should contain the same number of significant figures as the number with the fewest significant figures.
1.2 x 6.44 = 7.728, rather report it as 7.7.
Significant figures in addition and subtraction
In addition and subtraction, the final answer should contain the same number of decimal places as the number having the fewest number of decimal places.
Example: 11.125 + 6.1 = 17.225, it is better to report it as 17.2.
Significant figures when changing from decimal to scientific notation
When changing from decimal to scientific notation, we should maintain the same number of significant figures.
The use of Scientific Notation helps in eliminating ambiguous or non-significant zeros. For example, if 2900 is supposed to have three significant figures, then in scientific notation, we can represent it as 2.90×103. Similarly, we can write 0.0789 as 7.89×10−2, with 3 significant figures. The part of the representation that contains the significant figures (2.90 or 7.89) is called the significand or mantissa. The exponent part becomes irrelevant as far as the significant figures are concerned. Another example, 7.334 = 733.4 x 10-2 (both have 4 significant figures).
Significant figures in Logarithm and Antilogarithm
We shall restrict the discussion here to the logarithm to the base 10. We should round off the base-10 logarithm of a normalized number so that its decimal part (called the mantissa) has as many significant figures as the significant figures in the normalized number.
log10(7.0000 × 105) = log10(105) + log10(7.0000)
= 5.000000… + 0.84509804…
= 5.84509804 ≈ 5.84509.
The normalized number was 700000 (6 significant digits), so the decimal part of the answer should have the same number of figures.
The same rule applies while taking the antilogarithm.
105.84509 = 6,99,987.04114807… = 700000 = 7.0000 × 105.
How to know how many significant figures to use?
From the previous section, one should not conclude that we can truncate the numbers in the various calculation steps. Use a reasonable number of decimal places during the calculation steps and do the rounding off only when you have arrived at the final result.
Two examples with addition and multiplication operations:-
(7.1234 + 1.234) × 1.3 = 8.3574 × 1.3
= 10.86462 ≈ 10.9.
(7.1234 × 1.234) + 1.3 = 8.7902756 + 1.3
= 10.0902756 ≈ 10.1.
We did not compromise on decimal places in the intermediate stage.
Many people wonder if the treatment of significant figures would be different when doing mathematics, physics, or chemistry problems. In all these calculations, the underlying operation is some mathematics; hence the rules of the game remain the same.
Resources:
Several Resources on Significant Figures are freely available on the internet. Some great people have put their knowledge, thoughts, and work there for all to use.
Significant Figures Calculators
Even significant figure calculators (SFCs) have been designed and made available online. Some of the online significant figures calculators are below:
Byju’s Classes (the online tutorial)
You can access it from this link:
It is easy to use. Here is a snapshot of the calculator:
(Note: It uses javascript coding to calculate the significant figures. It is pretty easy to use. However, I could find a bug in it. I put the number ‘1000’ in the input field, and upon pressing Solve, I get ‘4’ as a result, which is wrong and as also by definition given by Byju’s themselves; see the highlighted part below:

The answer should have been ‘1’. Upon reading further, I found a disclaimer under the SFC.
“This calculator development is in progress some of the inputs might not work, Sorry for the inconvenience.”
Our advice: use it carefully at your peril, or do not use it until they withdraw the disclaimer.
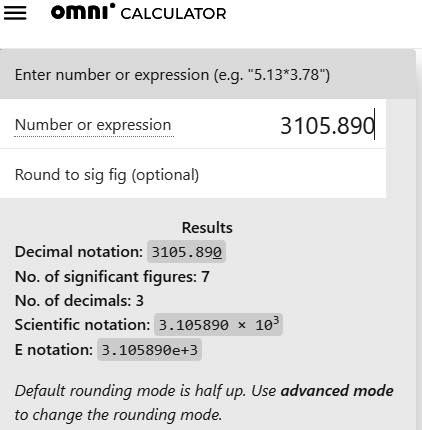
Omni Calculator
The most remarkable among others is the Omni Calculator (https://www.omnicalculator.com/math/sig-fig). It works ‘on-the-fly’; even as you start inputting the digits of a number, its significant figures and other relevant information begin to display. Here is a snapshot.
Calculator Soup
(https://www.calculatorsoup.com/calculators/math/significant-figures.php),
Sig Figs Calculator
(https://www.sigfigscalculator.com/)
Last but not least, Khan Academy’s video on significant figures,
https://www.khanacademy.org/math/arithmetic-home/arith-review-decimals/arithmetic-significant-figures-tutorial/v/significant-figures, takes the cake. The teacher’s style is very lucid, and the users have given it excellent reviews.
Author: Piyush Pandey

Former Administrator, Jawaharlal Nehru Memorial Fund, Anand Bhawan, Allahabad
Former Director, Nehru Planetarium, Worli, Mumbai
Former Assistant Director, Birla Planetarium, Kolkata
Founder Director Jawahar Planetarium, Anand Bhawan, Allahabad
Former Scientist, ARIES, Nainital