Torque

What is Torque?

Definition

Torque is the turning effect of force about a fixed point. It is also called the Moment of force.

Unit of torque

N-m

Dimension of torque

$[M{L^2}{T^{ - 2}}]$

Usual sign convention for torque

A torque that produces anticlockwise rotation is taken positive and clockwise rotation is taken negative.

Formula for torque

The magnitude of the torque is the product of the magnitude of the force and the perpendicular distance of the line of action of the force from the fixed point.

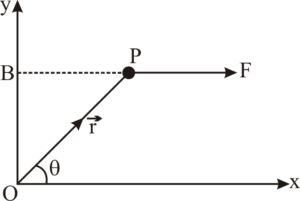
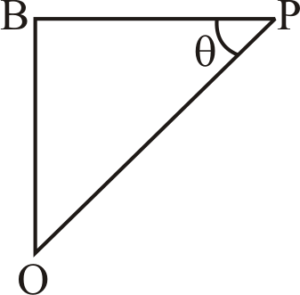
Torque of force F about the point O

${\Gamma _0} = OP \times F$

${\Gamma _0} = \left| {OP} \right|\,\left| F \right|\sin \theta \,\hat n$ …(i)

Now, from right angle triangle OBP,

$\sin \theta = \frac{{OB}}{{OP}}\quad \Rightarrow \quad OB = (OP)\sin \theta$

$or,\quad OB = \left| {OP} \right|\sin \theta$

Now, from (i),

${\Gamma _0} = (OB)(F)\hat n$

${\Gamma _0} = {r_1} \times F$

Some quick facts on torque

A force of a given magnitude applied at right angles to the door at its outer edge is most effective in producing rotation.

The moment of a force vanishes if either the magnitude of the force is zero or if the line of action of the force passes through the fixed point.

If the direction of force F is reversed, the direction of the moment of force is also reversed.

If the direction of both r and F is reversed, the direction of the moment of force remains the same.

Solved problems on Torque

Ex-1: A simple pendulum of length l is pulled aside to make an angle q with the vertical. Find the magnitude of the torque of the weight W of the bob about the point of suspension.

Ans. From figure, torque of weight W about point O,

${\Gamma _0} = {r_1} \times F$

$= (OP\sin \theta )(mg)( - \hat k)$

$= (\ell \,\sin \theta )(mg)( - \hat k)$

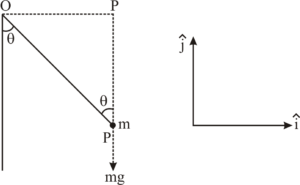
Therefore, the magnitude of torque of weight W about the point of suspension is

$\left| {{\Gamma _0}} \right| = mg\ell \sin \theta = W\ell \sin \theta$

Ex-2: A cubical block of mass m and edge a slides down a rough inclined plane of inclination q with a uniform speed. Find the torque of the normal force acting on the block about its center.

Ans. Since block is sliding with constant speed $mg\sin \theta = {f_k}$

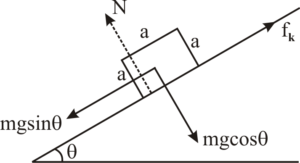
Again, cubical block has no any angular acceleration $(\alpha = 0)$

$\sum {{\Gamma _{cm}}} = 0\quad \Rightarrow \quad {\Gamma _{N,\,cm}} + {\Gamma _{{f_k},\,cm}} = 0$

$\Rightarrow \quad {\Gamma _{N,\,cm}} = \left( { - \frac{a}{2}{f_k}\sin {{90}^o}\hat k} \right)$

$\Rightarrow \quad \left| {{\Gamma _{N,\,cm}}} \right| = \frac{a}{2} \cdot mg\sin \theta$

Ex-3: If $F = (2N)\hat i - (3N)\hat j$ and $r = (3m)\hat i + (2m)\hat j$ , then find torque of force F about the origin.

Ans. As we know, ${\Gamma _0} = r \times F$

$r \times F = \left| {\begin{array}{*{20}{c}} {\hat i}&{\hat j}&{\hat k}\\ 3&2&0\\ 2&{ - 3}&0 \end{array}} \right| = \hat i(0 - 0) - \hat j(0 - 0) + \hat k( - 9 - 4) = ( - 13\,N{\rm{ - m}})\hat k$

So, torque of force F about the origin $= (13\,N{\rm{ - m}})( - \hat k)$ .

Moment of couple

A pair of equal and opposite forces with different lines of action is known as a couple. A couple produces rotation without translation. If an object is not on a pivot, a couple causes it to rotate about its center of mass.

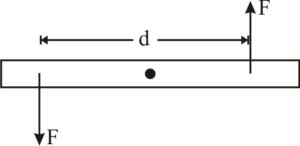
This couple can produce a turning effect or torque on the body. The moment of a couple is a measure of the turning effect (t).

$\Gamma$ = moment of couple = Magnitude of either force X perpendicular distance between the forces.

$\Gamma = Fd$

Mechanical equilibrium of a rigid body

A rigid body is said to be in mechanical equilibrium if its linear and angular momentum do not change with time or, equivalently, the body has neither linear nor angular acceleration.

Condition for translational equilibrium: No linear acceleration

The vector sum of the forces on a rigid body is zero.

${F_1} + {F_2} + ...... + {F_n} = \sum\limits_{i = 1}^n {{F_i}} = 0$

If the total force on the body is zero, then the total linear momentum of the body does not change with time;

$\sum P = {\rm{constant}}$

Condition for rotational equilibrium: No angular acceleration

The vector sum of all the torques on the rigid body is zero,

${\tau _1} + {\tau _2} + ...... + {\tau _n} = \sum\limits_{i = 1}^n {{\tau _i}} = 0$

If the total torque on the rigid body is zero, the total angular momentum of the body does not change with time.

The rotational equilibrium condition is independent of the location of the origin about which the torques are taken.

Sample problem: Mechanical equilibrium of a rigid body

Ex.:- An uniform meter stick of 200g is suspended from the ceiling through two identical strings of equal length fixed at the ends. A small object of mass of 20 grams is placed on the stick at a distance of 70 cm from the left end. Find tensions in two strings.

Ans.-Since the system is in equilibrium, so for translational equilibrium

$\sum {F_x} = 0,\,\,\sum {F_y} = 0$

${T_1} + {T_2} = (M + m)g$ …(i)

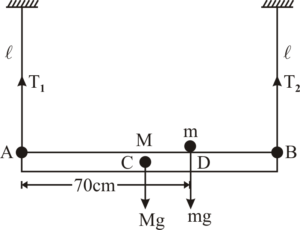
M = 200 gm, AB = 100 cm, AD = 70 cm, m = 20 gm.

Again, the system has no angular acceleration;

$\sum \Gamma = 0$

${\Gamma _{{T_1},\,A}} + {\Gamma _{Mg,\,A}} + {\Gamma _{mg,\,A}} = 0$

$(AB){T_2}\hat k + (AC)Mg( - \hat k) + (AD)mg( - \hat k) = 0$

$(AB){T_2} = (AC)Mg + (AD)mg$

$(100\,cm){T_2} = (50\,cm)Mg + (70\,cm)mg$

$\Rightarrow \quad 10{T_2} = 5Mg + 7mg$

Solving for ${T_2}$ ; ${T_2} = 1.12\,N$ .

Now, putting this value of ${T_2}$ into equation (i), we obtain ${T_1} = 1.04\,N$ .

Author

Rajesh Kumar

20 years of experience teaching high school and college physics to students across the globe.

When not teaching or mentoring, I write informative articles in physics and related subjects. So far, I have written more than 200 articles on different topics in physics. Apart from physics, I am proficient in engineering statics, dynamics, and calculus. I love spending time with my kids and listening to old Hindi songs.

Recent Posts

The Law of Conservation of Angular Momentum

Angular Momentum

Torque