Circular Motion

The animation below shows an object moving at a constant speed on a circular path. It is an example of Uniform Circular Motion as the object’s speed is constant. However, the direction of motion (along the tangent drawn at the point where the object is located at a particular moment) changes all the time, thus the velocity. We know the rate of change of velocity is called acceleration.

Fig. 1: Uniform Circular Motion: Animation (Credit)

In the animation above, the velocity is indicated by vector v (along the tangent), while the acceleration a is directed toward the center of motion.

If you are looking for a private 1:1 online tutoring session with an excellent Physics Tutor, feel free to contact us on WhatsApp, or else, please keep reading further.

Circular motion: Introduction

What is Circular motion?

If a point or an object moves along a circular path, its motion is called circular motion.

A circular motion requires some force. A force requires acceleration. This acceleration is called centripetal acceleration or radial acceleration.

Let us first see why a force is needed for the circular motion to occur.

Circular motion requires force

It becomes interesting to see this definition in the light of Newton’s First Law of Motion, which says, “An object at rest stays at rest, and an object in motion stays in motion with the same speed and the same direction unless acted upon; by an unbalanced force.”

Thus, we can deduce that some force must be present for a circular motion to occur.

The phrase ‘unbalanced force’ sounds peculiar, yet it is present all around us without realizing its significance. Think of a book kept on a table. The book is at rest. However, gravity acts vertically downwards, which gets ‘balanced’ by an equal and opposite force acting on it by the table – normal force (also called reaction, recall Newton’s third law of motion). One must apply a force to overcome the friction if one tries to slide the book along the table’s surface. This would now be called the case of ‘unbalanced’ force.

The preceding assumes that the motion occurs in an ideal state or space where no other forces exist. Therefore, the orientation of the circle where the motion is taking place does not matter, and it would be immaterial whether it is oriented horizontally or vertically. However, a little probing reveals the fallacy of this argument. The words ‘vertical’ or ‘horizontal’ presage the presence of gravity; we define vertical direction by suspending a bob from a string; the string is said to be vertically oriented. The plane perpendicular to this direction is the horizon, and any object moving in this plane is moving horizontally.

Similarly, we can conceive planes perpendicular to this horizontal plane; they are all vertical. Therefore, in a real-world situation, the treatment of circular motion gets modified by gravity. Let us try to explore it further with an example.

Example of circular motion

Take the case of a ball tied to a string, and you revolve it in a horizontal circle by giving small tugs of force in each revolution.

Fig 2: Horizontal Circular Motion

Consider an object of mass $m$ tied at one end of a string and moving in a horizontal circle of radius $r$ with a center at $O$ . The object is moving with a uniform linear velocity $v$ and angular velocity $\omega (v = r \omega)$ . The weight of the object $mg$ is acting vertically downwards. It is thus at right angles to the tension $T_s$ in the string. The force toward the center $O$ is:

$F = T_s = \frac {mv^2} {r} &=$ m $\omega^2$ r

Thus the tension in the string is equal to the centripetal force.

However, how did we conclude that centripetal acceleration (centripetal means center seeking or acting toward the center) should be equal to $\frac{v^2}{r}$ or $v\omega$ ? In most cases, you will find this term suddenly appearing as it is. It is not some gospel truth. Shouldn’t a curious mind like yours try to derive it? Let me help you out. Please look at the construction below.

Fig 3: Force and acceleration in Circular Motion

$O$ is the origin of the cartesian frame of reference, having axes as $OX$ and $OY$ . An object $P$ is moving such that it maintains a constant distance $r$ from the point $O$ , which means it performs the circular motion. It moves uniformly with magnitude $v$ on the circle with $r$ . It is making one complete revolution in $T$ seconds.

We can find out a few simple relationships. The distance traveled in time T is the circumference of the circle; thus, speed $v$ is given by:

$v &= \frac {2\pi r} {T}$ ——-[1]

Likewise, angular speed $\omega$ can be computed by dividing the total angle $2\pi$ (=360⁰) by the time taken ( $T$ ).

$\omega &= 2\pi T$ ——–[2]

Upon eliminating $T$ from equations [1] and [2] we get,

$v&=r\omega$ ——–[3]

Derivation of centripetal acceleration $\frac{v^2}{r}$ .

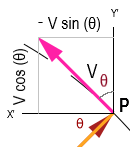
While the speed is uniform, the velocity (speed in a particular direction) is not so. It is a vector changing its direction at every point of the circle. The velocity $v$ has horizontal and vertical components. Please pay attention to the construction around point $P$ in the above diagram.

Let us pull a small segment of figure 3 here.

Recall the simple geometry you had learned, the alternate and complementary angles, and the line OP is inclined at angle $\theta$ to the $X$ -axis. Using a polar coordinate system (based on the angle around a pole), we can compute the horizontal $v_x$ and vertical $v_y$ components of the velocity at $P$ .

$v_x&=-v\sin\theta$ ; $v_y&=-v\cos\theta$
We can write, $v^2&= v_x^2 + v_y^2$

$&=(-v\sin\theta)^2 + (v\cos\theta)^2$

$&= v^2 (\sin\theta^2 + \cos\theta^2) = v^2$

Now is the turn to calculate the x and y components of the centripetal acceleration. Acceleration is the rate of change in velocity.

$a_x &= \frac{dv_x}{dt}=-v\sin\theta \frac{d\theta}{dt} =-v\omega\sin\theta$

$a_y&=v\omega\cos\theta$

Acceleration $a^2 = a_x^2 + a_y^2$ . From the above expressions we get,

$a^2 &= (- v \omega$ $\sin (\theta))^2 + (v \omega$ $\cos (\theta))^2$
$a^2 &= v^2 \omega^2 (\sin \theta ^2+ \cos \theta^2)$
$a^2 &= v^2 \omega^2$

$\Rightarrow a &= v \omega$

We can use the relation [3], $v= r\omega$ , and we get,

$a= r\omega^2 =\frac {v^2}{r}$

By using the relation [3] above, we can write,

You may also refer to the Khan Academy Video for the above and other derivations at this link.

Non-uniform circular motion

In a uniform circular motion, the particle’s speed and tension in the string tied to a bob remain constant. The velocity, which has the same magnitude as speed, keeps changing as the direction of the tangent drawn at the particle continuously changes.

Non-uniform circular motion is the motion of an object whose speed varies from point to point and does not cover the same distance in equal time intervals. This is irrespective of the time per cycle, which may be constant. In such a case, the particle has tangential and centripetal acceleration.

An example of a non-uniform circular motion is when you make a ball tied to a string move on a vertical circle, as shown in the illustration below.

Fig 4: Non-Uniform Circular Motion Simulation

In the illustration above, $OX$ – our baseline – is vertical, and the turning angle is $\theta$ . The weight $mg$ is acting vertically downwards. The acceleration, in this case, has two components, tangential and centripetal; both change with time. While the tangential acceleration $a_t$ is $g\sin\theta$ , the centripetal one is the string’s tension due to circular motion plus the gravity’s radial component ( $a_r$ ) getting added vectorially to the string tension or the centripetal force.

Consider two unique situations; one at the bottom point where $\theta=0$ . Thus $\sin0= 0$ . Therefore the contribution of gravity to the tangential component is zero. The other point is at the top; here, $\theta$ is 180⁰, and $\sin180= 0$ . So the tangential component in both the cases is zero. The tension is thus maximum at the bottom ( $\frac {mv^2} {r} + mg$ ), whereas it is the lowest at the top ( $\frac {mv^2} {r} - mg$ ). It varies cyclically between these two extreme values.

Circular-Motion Free Body Diagram

Before discussing this specific case, we should know what the free body diagram is all about. If we draw a diagram showing only the forces acting on a body (or a collection of bodies acting as one) and not the objects in its surroundings, then such a diagram is called the free body diagram. In a free body diagram, care should be taken to draw the length of the arrows as they indicate the magnitude of force.

Consider two cases; a block of wood sitting at rest on a table and another on a ramp. See below on the right the free body version of the diagrams on the left.

Fig 5: Free body diagram of an object resting on a table.

Here $mg$ is the gravitational force, and $R$ is the normal (also called reaction) from the table.

Fig 6: Free body diagram of an object resting on a ramp.

Here $F_r$ is the frictional force, $R$ is the normal (force of reaction) from the ramp, and $mg$ is the gravitational force.

Fig 7: Free-body diagram in a horizontal circular motion

Radial and tangential accelerations in a uniform circular motion

From the above discussions, we can summarize that the radial acceleration $a_r= \frac {v^2} {r}$ and the tangential acceleration $a_t$ is 0. Even though the velocity changes continuously, it changes only its direction and not magnitude.

Dynamics of circular motion

Figure 8: Dynamics of Circular Motion

In the above 3 situations, the velocity is tangential to the circle. Hence, the resultant force and the acceleration are directed towards the center.

We have noted that in a circular motion, the direction of motion is tangential and constantly changing, but the speed is constant.

The force required to accelerate or change the object’s velocity is always towards the center and perpendicular to the motion.

The centripetal force vector is always perpendicular to the instantaneous velocity vector and does not produce any work. This means that the total mechanical energy of the particle remains constant.

Uniform Circular Motion and Simple Harmonic Motion

The following GIF, courtesy of Kaiserscience, beautifully displays it.

The one-dimensional projection of a ball moving on a vertical circle onto the x-axis visualizes a linear simple harmonic motion effect.

Planetary Motion: Solar System- Rotation and Revolution

The circle is a class of ellipses with its eccentricity as zero. The word eccentricity in science means a departure from being a perfect circle. In cartesian geometry, the formula of an ellipse is given by:

$\frac{x^2}{a^2} + \frac{y^2}{b^2} &=1$ where $a$ and $b$ are the semi-major and semi-minor axes of the ellipse. Without going into the definition of an ellipse, we write here the formula for eccentricity, $e$ ,

$e &= \sqrt {{1- \frac {b^2} {a^2}}$

In the case of a circle, $a = b = 1$ , and hence the eccentricity $e = 0$ ; the eccentricity of an ellipse is always less than zero since $b < a$ .

It is evident that the circle is a particular class, and nature instead prefers variety. With a given distance from a center, you can draw only one circle but an infinity of ellipses.

The planetary orbits display this nature preference; hence they are ellipses. Let us take the case of the orbit of the Earth around the Sun. It has an eccentricity of $e\approx 0.017$ . You will draw a circle if you try to draw an ellipse of this eccentricity value. This small eccentricity of Earth’s orbit brings about only a 3.3% overall variation in the Earth’s distance from the Sun. The average distance between the Earth and Sun is 149,598,262 km (you may memorize it as 150 million km, 93 million miles, 8.3 light-minutes, or 500 light-seconds). The average distance between the Earth and Sun is 1 AU (Astronomical Unit). When the Earth is the closest to the Sun (called the perihelion, which falls around the 4th of January every year), then its distance from the Sun is 0.98 AU, and at aphelion (when it is the farthest from the Sun around the 4th of July every year) it is 1.02 AU. Thus we see that the departure from an ellipse is minimal. You may regard the Earth as an object moving in a circle of radius 1 AU with a speed of 29.78 km/s (107,208 km/h; 66,616 mph). You may memorize it as 30 km/s. However, most of the time, the speed of Earth is different from this value. At perihelion, it is maximum and gradually decreases to become minimum at aphelion passage. Imagine we are always traveling in space with an average speed of 30 km/s, without even realizing it!

The orbits of other planets of the solar system are also elliptical, and the most peculiar among them is that of a body that is no longer regarded as a planet – you guessed it right – Pluto. Its orbital eccentricity is 0.248, and its orbital tilt of 17⁰ (to the ecliptic, the Earth’s orbital plane around the Sun); these two factors, along with its small size, were the contributing factors to its ‘ouster’ from the solar system. Compare these data with Earth’s. Earth has an orbital eccentricity of 0.017 and its rotational axis (on which it turns once in 23 hours, 56 minutes, and 4 seconds, ~23.9 hours). Even this little eccentricity conspires with the inclination of its rotational axis to its orbital plane, 23.45⁰, to effect the change of seasons we are so familiar with.

Planet	e	P(AU)	A(AU)	T(axis) Days	T(sun) Days
Mercury	0.206	0.31	0.47	58.6	87.97
Venus	0.007	0.718	0.728	243	224.7
Earth	0.017	0.98	1.02	0.99	365.26
Mars	0.093	1.38	1.67	1.03	1.88
Jupiter	0.048	4.95	5.45	0.41	11.86
Saturn	0.056	9.02	10	0.45	29.46
Uranus	0.047	18.3	20.1	0.72	84.01
Neptune	0.009	30	30.3	0.67	164.79
Pluto	0.248	29.7	49.9	6.39	248.59

Table: Planetary Data

(Source: NASA, Exploratorium.Edu)

Symbols used:

e=Eccentricity

P(AU)=Perihelion Distance in AU (closest point to the Sun)

A(AU)=Aphelion Distance in AU (farthest point from the Sun)

T(axis)=Rotation Period (on its axis)

T(sun)=Revolution Period around the sun

Figure 9: Courtesy: NOAA (National Oceanic and Atmospheric Administration). The ellipse showing Earth’s orbit is exaggerated in eccentricity. The point at which a planet is closest to the sun is called perihelion. The farthest point is called aphelion. Similarly, Moon’s closest and farthest approaches to Earth are called perigee and apogee, respectively (where ‘gee’ stands for Earth).

Figure 10: Image credit: New Mexico State University, Astronomy Department.

The cause of the seasons on Earth is self-explanatory; we learned it in lower school.

Many-body-problem and perturbations, satellites, and planetary missions

The motion of Earth around the Sun and, for that matter, that of any other planet of the solar system can be regarded as a two-body problem only to a certain extent for rudimentary purposes only. In reality, the Earth is not only influenced by the gravity of the Sun but also by that of the other planets. The planets move in their elliptical orbits, with mercury taking the shortest time of 88 days per revolution, our Earth takes what we call a year, and the farthest planet, Neptune, takes 165 Earth-years. The remote Pluto, which was regarded as a planet till 2006 and then categorized as a dwarf planet, takes 249 years to once around the Sun. Its highly eccentric orbit brings it inside to orbit of Neptune for about 20 years in each cycle.

When interplanetary missions are sent to Mars, Jupiter, or beyond, intricate calculations are done to design the mission trajectory, including all tugs and pulls of the objects it passes by (called perturbations in Physics).

Rotation and Revolution

These two terms are used synonymously, but in physics, particularly astronomy, rotation often refers to a planet turning on its axis to maintain clarity. In contrast, the word revolution is reserved for the motion of planets and other solar system bodies in their respective orbits around the Sun.

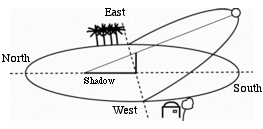
Movement of the shadow of a vertical pole

As the sun rises somewhere on the eastern horizon, traces and circular arc through the sky, and sets on the western horizon, the shadow of a vertical pole traces a path on the ground. It is a straight line only on two days during the year, on the spring equinox (around 21 March) and the autumnal equinox (around 23 September). On the rest of the days of the year, it traces different unique arcs.

Figure 11: The above picture shows the shadow of a pole when the Sun is highest in the sky at local noon. Courtesy: https://pwg.gsfc.nasa.gov/).

Figure 12: Length and direction of the shadow of a pole with height h. (by author)

Figure 13: The picture above shows the Sun’s path across the sky on 4 chosen dates; summer solstice (red curve), spring and autumnal equinoxes (same blue curve), and winter solstice (green curve). Courtesy: https://pwg.gsfc.nasa.gov/).

Can you figure out what would be the locus of the position of the Sun at the same time (as given by your watch), say at noon? Well, it turns out to be somewhat like the figure of eight (8).

Explanation: Our clocks or watches tell us the civil time; they are made to run at the same constant rate. But the Sun doesn’t. We have discussed above that the speed of the Earth in its orbit (average ~ 30 km/s) varies as it goes on its annual journey; it is fastest in January and slowest in July. This means the apparent speed of the Sun around Earth varies in the same fashion. So it reaches the meridian sometimes earlier or later than the average time. This, along with the fact that due to the axial inclination of the Earth, the Sun’s height in the sky at noon.

Fig. 14: Astrophotographer Giuseppe Petricca took the image from Sulmona, Abruzzo, Italy. The dots forming a curved figure-8 in the sky mark where the sun appeared every day at the same time in a pattern called an analemma. (Image credit: http://www.gmrphotographer.net and www.space.com). This strange figure of the sun creating a figure-eight shape in the sky is an incredible sight but requires a year of patience by this dedicated photographer to create. Such a figure is called the analemma in astronomy.

This is how Sun appears around the meridian at the same clock time over the year.

Another question is what path the tip of a pole traces on the ground in an entire year. Let us take the case of a place on the equator (say, the city of Quito in Ecuador).

Fig 15: The vertical rod is at point A; the light blue (cyan) straight line is the locus of the shadow on the two equinoxes (it would produce a zero shadow at local noon). North is at the top. The curved lines in blue and red color are the locus of the shadows on two extreme dates, winter and summer solstice, respectively. The shadows trace curved paths between these two curves on other year dates—an image created with Shadows software (https://www.shadowspro.com/.

Fig 16: This detailed diagram is drawn for the latitude of Berlin, 15.50 N, with a longitude of 13.40 E. the location of the pole is shown by a red circle and that of the tip of the shadow by the yellow circle. This shadow refers to 20 October or 21 February, both at 15:45. The hour marks are indicated by numbers, black dots, and figures of 8s. Notice that the blue line marking noon is not at noon but is close to where the 13-hour mark should be. The reason this is a longitude corrected dial. The longitude of 13.40 E means that Berlin is located as many degrees to the East of the Greenwich meridian. Therefore, the sun reaches the overhead position in Belin much before London, by 13.4 x 4 = ~ 54 minutes (3600 = 24 hours = 1440 minutes, thus 10 = 4 minutes) earlier, which is close to 13 hours or 1 pm. The figures of 8s are the manifestation of the sky movement of the Sun that we saw in Figure 14. For any particular time marker, the shadow travels on the blue part of a particular figure after the autumnal equinox and the red part after the spring equinox. The curved lines are labeled with dates like 12/21 (winter solstice on 22 December), 11/22 (22 November), etc. We call this sundial, analemmatic sundial; it gives not only the time but also the date. Image courtesy: http://www.jgiesen.de/analemma.

OTHER RESOURCES

https://acejee.com/blog/uniform-non-uniform-circular-motion/https://www.animations.physics.unsw.edu.au/jw/circular.htm#acceleration https://kaiserscience.files.wordpress.com/2015/09/shm-circular-motion-to-linear-motion-gif.gif?w=960 https://www.askmattrab.com/notes/1280-motion-in-horizontal-circle https://amsi.org.au/teacher_modules/Circle_Geometry.html Circular Motion Applet NASA

Author: Piyush Pandey
Former Administrator, Jawaharlal Nehru Memorial Fund, Anand Bhawan, Allahabad
Former Director, Nehru Planetarium, Worli, Mumbai
Former Assistant Director, Birla Planetarium, Kolkata
Founder Director Jawahar Planetarium, Anand Bhawan, Allahabad
Former Scientist, ARIES, Nainital

Author

Piyush Pandey

Former Administrator, Jawaharlal Nehru Memorial Fund, Anand Bhawan, Allahabad

Former Director, Nehru Planetarium, Worli, Mumbai

Former Assistant Director, Birla Planetarium, Kolkata

Founder Director, Jawahar Planetarium, Anand Bhawan, Allahabad

Former Scientist, ARIES, Nainital

Recent Posts

Circular Motion

Number types in Math

Significant figures