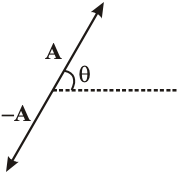Vectors in Physics

Vectors are part of everyday life. When any person gives you directions, he may say something like; the school is 3 km that way and point. He gives you both a magnitude (a measurement) and a direction (by pointing). Vectors in Physics is an essential concept that one must master.

Plenty of situations in our life display vectors, and plenty of ideas in physics are vectors, too, for example, velocity, acceleration, and force, displacement. Vectors are fundamental.

Before we talk about vectors, let us talk about Physical Quantities first.

Physical Quantities:

The quantities that are measurable are called physical quantities. Ex. Length, mass, time, velocity. These quantities can be vectors, scalars, or tensors.

Vectors :

Vectors are those which have both magnitude and direction and also obey laws of vector addition.

Ex: Velocity, force momentum, torque, etc.

Scalars :

Scalars are those which have only magnitude.

Ex: Mass, Time, Distance, Flux.

Note: a physical quantity having magnitude and direction but not obeying the law of vector addition is treated as a scalar. Ex: Electric current is a scalar quantity.

Electric current is always associated with direction, but it is not a vector quantity. It does not obey the law of vector addition.

The resultant of i₁ and i₂ is (i₁+ i₂) by Kirchoff’s current law. The resultant does not depend on the angle between currents i₁ and i₂.

Tensors :

Tensors are those quantities having different magnitudes in different directions. These do not obey the laws of vector addition.

Ex: the moment of inertia, stress, etc.

Now let us discuss Vectors in detail.

More about Vector Quantities

Directions and magnitude of a vector :

When we have a vector, we must keep in mind two quantities: its direction and magnitude.

We see vectors drawn as arrows in physics, which is perfect because an arrow has both a clear direction and a clear magnitude (the length of the arrow)

The arrow represents a vector that starts at the foot and ends at the head.

In physics, we use A to represent a vector. In some books, we see it with an arrow on top A. The arrow means that this is not only a scalar value which would be represented by A but also something with direction.

Why are vectors important?

Vectors are used in many branches of physics whenever there are quantities that we must describe in both magnitude and direction.

Vectors are used in many areas. E.g.:

Vectors in physics
vectors in kinematics
vectors in engineering mechanics
vectors linear algebra
vector geometry etc.

The laws of electromagnetism and Maxwell’s equations are expressed in terms of vectors and vector field concepts. Vector operators such as the Gradient, divergence, and curl are often used in physics. Operations such as cross product and the dot product have many examples in physics. The cross product describes the Lorentz force, and mechanical work is expressed as the dot product of displacement and force vectors.

There is no division of vectors. Why?

Vectors are quantities with magnitudes as well as direction. Dividing a vector by another vector means we are dividing a direction by another direction, just like if we divide east by west. This does not make sense.

What is the triangle law of vector addition?

The triangle law of vector addition says that when two sides of the triangle represent two vectors with the order of magnitude and direction, the third side of the triangle represents the magnitude and direction of the resultant vector.

C is also known as the resultant vector.

Parallelogram rule of vector addition :

The parallelogram rule of vector addition says that if two vectors are assumed to be the adjacent sides of a parallelogram, then the resultant of these two vectors is given by the vector that is diagonal, passing through the contact point of two vectors (tail to tail).

C is also called the resultant of a and b.

Vector arithmetic :

Addition of vectors :

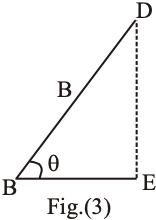
Let A and B be the two vectors to be added. A diagram is drawn in which the starting point of B coincides with the ending point of A.

Here (A + B) is the resultant of A and B (triangle rule of vector addition).

Now, the same rule can be stated in a slightly different way. We draw the vectors A and B with both starting points coinciding, considering these two vectors as the adjacent sides. We complete parallelogram. The diagonal through the common tails give the sum of two vectors.

From fig 1, we can say AB + AC = AD.

Let, |A| = A and |B| = B.

|A| : magnitude of A & |B| : magnitude of B.

We are interested in calculating the magnitude and direction of (A + B).

Let the angle between A and B is $\theta$ .

From fig.3,

$\cos \theta = \frac{{BE}}{B}$

$BE = B\cos \theta$

$DE = B\sin \theta$

Now, from fig.2, from right angle triangle AED.

$A{D^2} = {(AE)^2} + {(ED)^2}$

$A{D^2} = {(AB + BE)^2} + {(ED)^2}$

$A{D^2} = {(A + B\cos \theta )^2} + {(B\sin \theta )^2}$

So, magnitude of (A + B) is |A + B| $= \sqrt {{A^2} + {B^2} + 2AB\cos \theta }$

The angle made by the resultant vector with A can be found from the right angle triangle AED.

$\tan \theta = \frac{{DE}}{{AB}} = \frac{{B\sin \theta }}{{B\cos \theta + A}}$

Multiplication of a vector by a number :

Let A is a vector of magnitude A and C be a number. We define the vector B = CA as a vector of magnitude $\left| {CA} \right|$ .

If C is positive, the direction of the vector B = CA is the same as that of A.

Multiplication by (–1) inverts the direction of the vector. The vectors A and –A have equal magnitudes but opposite directions.

Subtraction of vectors :

Let A and B be two co-initial vectors, as shown in the figure.

We define (A – B) as the vector A and (–B) sum. For subtracting B from A, we invert the direction of B and add to A.

Here, the angle between A and –B will be (180º– $\theta$ ).

Unit vectors :

It is a vector whose magnitude is unity. A unit vector parallel to a given vector R is given by, $\hat R = \frac{{\bf{R}}}{{|{\bf{R}}|}}$ .

$\hat R$ represents the sense of direction of the vector R.

A unit vector is a dimensionless physical quantity.

The unit vector along ${\bf{R}} = x\hat i + y\hat j + z\hat k$ can be written as

$\hat R = \frac{{\bf{R}}}{{|{\bf{R}}|}} = \frac{{x\hat i + y\hat j + z\hat k}}{{\sqrt {{x^2} + {y^2} + {z^2}} }}$

Here, R is the given vector, and |R| is the magnitude of that vector.

Orthogonal Unit vectors :

$\hat i$ , $\hat j$ , and $\hat k$ are orthogonal unit vectors.

$\hat i$ is known as a unit vector along the x-axis.

$\hat j$ is known as a unit vector along the y-axis.

$\hat k$ is known as a unit vector along the z-axis.

Null vector or zero vector :

It is a vector of zero magnitude.

Its direction is indeterminate.

It is represented as O.

Position vector :

It is a vector that represents the position of a particle with respect to the origin of a coordinate system. The position vector of a point (x, y, z) can be written in the form:

${\bf{R}} = x\hat i + y\hat j + z\hat k$ .

Resolution of a vector :

The figure shows a vector OP in the x-y plane drawn from the origin O. The vector makes $\alpha$ angle with the x-axis and $\beta$ angle with the y-axis. PA is perpendicular drawn from point P on the x-axis, and PB is the perpendicular drawn from point P on the y-axis. The length OA is the projection of OP on the x-axis, and the length OB is the projection of OP on the y-axis.

According to the parallelogram rule of vector addition

OP = OA + OB ….(1)

Here OP is resolved in two parts. OA is along the x-axis, and OB is along the y-axis.

Eqn. (1) can be written in the form,

${\bf{OP}} = OP(\cos \alpha )\hat i + OP(\cos \beta )\hat j$

${\bf{R}} = R\cos \alpha \hat i + R\cos \beta \hat j$

The quantity $OP(\cos \alpha )$ is known as the x-component of OP, and the quantity $OP(\cos \beta )$ is known as the y-component of OP. See this Khan academy video on vector resolution for a better understanding.

Definition of Resolution of a vector :

Splitting up a single vector into two or more vectors is known as the resolution of a vector.

If the vector R is not in the x-y plane, this may have non-zero projections along the x, y & z-axis. Therefore, we can resolve this into three parts (along the x-axis, y-axis, and z-axis).

If $\alpha ,\,\,\beta \,\,\& \,\,\gamma$ be the angles made by vector R with x, y and z axis respectively, then we can write

${\bf{R}} = (R\cos \alpha )\hat i + (R\cos \beta )\hat j + (R\cos \gamma )\hat k$

$\hat i,\,\,\hat j\,\,\& \,\,\hat k$ are unit vectors along x-axis, y-axis and z-axis respectively.

The value $R\cos \alpha$ is called a component of R along the x-axis.

The value $R\cos \beta$ is called a component of R along the y-axis.

The value $R\cos \gamma$ is called a component of R along the z-axis.

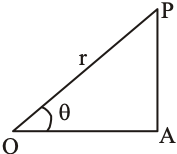
The polar form of vector :

When we know a point in Cartesian coordinate (X, Y) and want it in polar coordinates $(r,\,\theta )$ , we solve a right angle triangle with two known sides.

Suppose, there is a point $({X_0},\,{Y_0})$ in x-y plane.

From the triangle rule of vector addition,

OP = OA + AP

${\bf{OP}} = {X_0}\hat i + {Y_0}\hat j$

Again, from right angle triangle OAP,

$O{P^2} = O{A^2} + A{P^2}$

$O{P^2} = X_0^2 + Y_0^2$

$\quad OP = \sqrt {X_0^2 + Y_0^2}$

$r = \sqrt {X_0^2 + Y_0^2}$

We call OP length as r, from given triangle POA,

$\tan \theta = \frac{{PA}}{{OA}} = \frac{{{Y_0}}}{{{X_0}}}$

So, the vector representation.

${\bf{OP}} = {X_0}\hat i + {Y_0}\hat j$ is $(r,\,\theta )$ in polar form vector

We can write this as

${\bf{OP}} = \left( {\sqrt {X_0^2 + Y_0^2} ,\,{{\tan }^{ - 1}}\frac{{{Y_0}}}{{{X_0}}}} \right)\,\, \Rightarrow$ Polar form of a vector.

${\hat e_r}$ is the unit vector along the radial direction, and ${\hat e_t}$ is the unit vector along the tangential direction.

Multiplication of vectors :

A vector multiplied by another vector may give a scalar or a vector. Hence there are two types of products for the multiplication of two vectors.

(a) dot product or scalar product.

(b) cross product or vector product.

Scalar product or dot product :

The scalar product of two vectors A and B is given by ${\bf{A}} \cdot {\bf{B}} = |{\bf{A}}||{\bf{B}}|\cos \theta = AB\cos \theta$ , where $\theta$ is the smaller angle between A & B.

The quantity $A\cos \theta$ is known as a component of A along B, and the quantity $B\cos \theta$ is known as a component of B along A.

Properties of Scalar product :

(i) Scalar product is commutative i.e., ${\bf{A}} \cdot {\bf{B}} = {\bf{B}} \cdot {\bf{A}}$

(ii) scalar product is distributive ${\bf{A}} \cdot ({\bf{B}} + {\bf{C}}) = {\bf{A}} \cdot {\bf{B}} + {\bf{A}} \cdot {\bf{C}}$

(iii) It does not obey associative law i.e., we can not write ${\bf{A}} + ({\bf{B}} + {\bf{C}}) = ({\bf{A}} + {\bf{B}}) + {\bf{C}}$

Scalar product of two parallel vectors is maximum ${\bf{A}} \cdot {\bf{B}} = |{\bf{A}}||{\bf{B}}|\cos \theta = AB$ if $\theta = 0$

The scalar product of two perpendicular vectors is zero.

${\bf{A}} \cdot {\bf{B}} = 0$ if ${\bf{A}} \bot {\bf{B}}$ .

The scalar product of two opposite vectors is negative and minimum.

Scalar product of two vectors is negative if $180 > \theta > 90$ .

In the case of orthogonal unit vectors.

$\hat i \cdot \hat i = \hat j \cdot \hat j = \hat k \cdot \hat k = 1$

$\hat i \cdot \hat j = \hat j \cdot \hat k = \hat k \cdot \hat i = 0$

In terms of components of vectors

If ${\bf{A}} = {A_x}\hat i + {A_y}\hat j + {A_z}\hat k$ and ${\bf{B}} = {B_x}\hat i + {B_y}\hat j + {B_z}\hat k$

Then ${\bf{A}} \cdot {\bf{B}} = {A_x}{B_x} + {A_y}{B_y} + {A_z}{B_z}$

Also, ${\bf{A}} \cdot {\bf{A}} = A_x^2 + A_y^2 + A_z^2 = {A^2}$

And magnitude of A can be written as $|{\bf{A}}| = A = \sqrt {A_x^2 + A_y^2 + A_z^2}$

If ${\bf{A}} \bot {\bf{B}}$ then ${\bf{A}} \cdot {\bf{B}} = 0$

$\Rightarrow \quad {A_x}{B_x} + {A_y}{B_y} + {A_z}{B_z} = 0$

Application of Dot Product :

(i) Angle between two vector A & B can be found from $\cos \theta = \frac{{{\bf{A}} \cdot {\bf{B}}}}{{|{\bf{A}}| \cdot |{\bf{B}}|}}$

(ii) Vector component of A along B is $= \frac{{{\bf{A}} \cdot {\bf{B}}}}{B}\hat B$

(iii) Vector component of B along A is $= \frac{{{\bf{A}} \cdot {\bf{B}}}}{A}\hat A$

(iv) the component of A perpendicular to B in the same plane is ${\bf{C}} = {\bf{A}} - \frac{{{\bf{A}} \cdot {\bf{B}}}}{B}\hat B$

(v) the component of B perpendicular to A in the same plane is ${\bf{D}} = {\bf{B}} - \frac{{{\bf{A}} \cdot {\bf{B}}}}{A}\hat A$ .

Vector product or cross product :

If A and B are two vectors and angle between them is $\theta$ , then cross product of these two vectors is given by ${\bf{A}} \times {\bf{B}} = AB\sin \theta \,\hat n$

Where $\hat n$ is a unit vector perpendicular to the plane containing A & B.

Case-I: If two vectors are parallel $(\theta = 0)$ or antiparallel $[\theta = (180)]$ then ${\bf{A}} \times {\bf{B}} = 0$ .

Case-II: If two vectors are perpendicular to each other $\theta = 90$ then $|{\bf{A}} \times {\bf{B}}| = AB$ (maximum).

The Cross product of two vectors is a vector quantity. We can obtain the direction of the cross product of two vectors with the help of the right-hand thumb rule or right-hand screw rule.

Right-hand screw rule :

Consider a right-handed screw to be placed along the normal of the plane containing the two vectors. Rotate the cap of the screw from the first vector to the second vector via the smallest angle between them; the direction of motion of the tip of the screw gives the direction of their vector product.

Right hand thumb rule :

Consider the normal to the plane of the two vectors to be held in the right hand with the thumb erect. If the fingers are whirling in the direction from the first vector to the second vector through the smallest angle between them, the direction of the thumb gives the direction of the vector product.

Properties of vector product :

(a) cross product does not obey commutative law ${\bf{A}} \times {\bf{B}} \ne {\bf{B}} \times {\bf{A}}$ but ${\bf{A}} \times {\bf{B}} = - {\bf{B}} \times {\bf{A}}$

(b) cross product obeys distributive law ${\bf{A}} \times ({\bf{B}} + {\bf{C}}) = {\bf{A}} \times {\bf{B}} + {\bf{A}} \times {\bf{C}}$

(c) cross product do not obey associative law ${\bf{A}} \times ({\bf{B}} \times {\bf{C}}) \ne ({\bf{B}} \times {\bf{A}}) \times {\bf{C}}$

If $\hat i,\,\,\hat j,\,\,\hat k$ are unit vectors then

$\hat i \times \hat i = \hat j \times \hat j = \hat k \times \hat k = 0$

$\hat i \times \hat j = \hat k,\,\,\hat j \times \hat k = \hat i,\,\,\hat k \times \hat i = \hat j$

$\hat j \times \hat i = - \hat k,\,\,\hat k \times \hat j = - \hat i,\,\,\hat i \times \hat k = - \hat j$

If ${\bf{A}} = {A_x}\hat i + {A_y}\hat j + {A_z}\hat k$

${\bf{B}} = {B_x}\hat i + {B_y}\hat j + {B_z}\hat k$

Then ${\bf{A}} \times {\bf{B}} = \left| {\begin{array}{*{20}{c}} {\hat i}&{\hat j}&{\hat k}\\ {{A_x}}&{{A_y}}&{{A_z}}\\ {{B_x}}&{{B_y}}&{{B_z}} \end{array}} \right|$

$= \hat i({A_y}{B_z} - {A_z}{B_y}) - \hat j({A_x}{B_z} - {A_z}{B_x}) + \hat k({A_x}{B_y} - {A_y}{B_x})$

Unit vector normal to both A and B is $\hat n = \frac{{{\bf{A}} \times {\bf{B}}}}{{|{\bf{A}} \times {\bf{B}}|}}$

If two vectors, A and B, are parallel

$\frac{{{A_x}}}{{{B_x}}} = \frac{{{A_y}}}{{{B_y}}} = \frac{{{A_z}}}{{{B_z}}} = {\rm{constant}}$

Projection of a vector :

Q.
If ${\bf{A}} = 2\hat i + 3\hat j$ and ${\bf{B}} = 2\hat j + 3\hat k$ , find the projection of B along A.

Ans.
As we know that ${\bf{A}} \cdot {\bf{B}} = |{\bf{A}}|\,|{\bf{B}}|\cos \theta$

${\bf{A}} \cdot {\bf{B}} = AB\cos \theta$

Projection of B along A equals to $B\cos \theta$

$\quad B\cos \theta = \frac{{{\bf{A}} \cdot {\bf{B}}}}{A} = \frac{{{\bf{A}} \cdot {\bf{B}}}}{{|{\bf{A}}|}}$

$\quad B\cos \theta = \frac{6}{{\sqrt {{2^2} + {3^2}} }} = \frac{6}{{\sqrt {13} }}$

Vectors normals to a plane :

Q.
Find the unit vector perpendicular to ${\bf{A}} = 3\hat i + 2\hat j$ and ${\bf{B}} = \hat i - \hat j$ .

Ans.

As we know, ${\bf{A}} \times {\bf{B}} = |{\bf{A}}|\,|{\bf{B}}|\sin \hat n$

$\frac{{{\bf{A}} \times {\bf{B}}}}{{|{\bf{A}} \times {\bf{B}}|}} = \hat n$

Here $\hat n$ is a vector perpendicular to the x-y plane.

Now, ${\bf{A}} \times {\bf{B}} = \left| {\begin{array}{*{20}{c}} {\hat i}&{\hat j}&{\hat k}\\ 3&2&0\\ 1&{ - 1}&0 \end{array}} \right| = \hat i\,(0 - 0) - \hat j\,(0 - 0) + \hat k\,( - 3 - 2) = 5\,( - \hat k)$ .

$\quad \hat n = \frac{{ - 5\,(\hat k)}}{5} = ( - 1)\,\hat k$

So, $\hat n = ( - 1)\,\hat k$ .

Two vectors are perpendicular or orthogonal if :

Q.
If the vectors ${\bf{A}} = a\,\hat i + a\,\hat j + 3\,\hat k$ and ${\bf{B}} = 2a\,\hat i - 2\,\hat j - \,\hat k$ are perpendicular to each other then find the positive value of a.

Ans.
As we know, two vectors will be perpendicular only when ${\bf{A}} \cdot {\bf{B}} = 0$ .

$(a\,\hat i + a\,\hat j + 3\,\hat k) \cdot (2a\,\hat i - \hat j - \hat k) = 0$

$2{a^2} + (a)\,( - 1) + (3)\,( - 1) = 0$

$2{a^2} - a - 3 = 0$

$2{a^2} - 3a + 2a - 3 = 0$

$a(2a - 3) + 1(2a - 3) = 0$

$\Rightarrow \,\,\,a = \frac{3}{2};\,\,a = - 1$

So, the positive value of a will be $\frac{3}{2}$ .

Two vectors are parallel if :

Q.
What is the condition for the vectors $2\hat i + 3\hat j + 4\hat k$ and $3\hat i - a\hat j + b\hat k$ to be parallel?

Ans.
If two vectors ${\bf{A}} = {x_1}\hat i + {y_1}\hat j + {z_1}\hat k$ and ${\bf{B}} = {x_2}\hat i + {y_2}\hat j + {z_2}\hat k$ will be parallel only

when, $\frac{{{x_1}}}{{{x_2}}} = \frac{{{y_1}}}{{{y_2}}} = \frac{{{z_1}}}{{{z_2}}}$ .

Similarly, for given question, both vectors will be parallel only when $\frac{2}{3} = \frac{3}{{ - a}} = \frac{4}{b}$

This is the necessary condition.

Not sure how to solve vectors in physics problems? You are not alone. Connect with an online physics tutor for a private 1:1 tutoring session right away!

Author

Rajesh Kumar

20 years of experience teaching high school and college physics to students across the globe.

When not teaching or mentoring, I write informative articles in physics and related subjects. So far, I have written more than 200 articles on different topics in physics. Apart from physics, I am proficient in engineering statics, dynamics, and calculus. I love spending time with my kids and listening to old Hindi songs.

Recent Posts

The Law of Conservation of Angular Momentum

Angular Momentum

Torque