Introduction
Most students assume their calculus struggles stem from calculus itself—that derivatives and integrals are simply too abstract or difficult. The uncomfortable truth? Calculus isn’t the problem. Algebra is.
Across multiple research studies and university instructor surveys, educators consistently identify the same pattern: students who fail calculus rarely fail because they don’t understand calculus concepts. They fail because foundational algebra gaps sabotage them before they even reach calculus-specific material. A comprehensive study on calculus prerequisite knowledge found that errors in algebraic manipulations hindered correct solutions to calculus problems even when students completed the calculus portion accurately. In fact, students in introductory calculus frequently encounter the paradox of “understanding the concept but making computational errors” and nearly every error traces back to missed or misunderstood algebra.
The good news? These gaps are entirely fixable. Identifying the five most common algebra mistakes now before or while taking calculus transforms your entire trajectory.
Need expert learning support? Check out our online tutoring
The Algebra-Calculus Connection: Why It Matters
Calculus requires you to manipulate algebraic expressions fluently. When you compute a derivative using the power rule, you’re applying algebraic exponent laws. When you integrate using u-substitution, you’re performing algebraic factoring. When you solve optimization problems, you’re manipulating formulas algebraically. Every single calculus problem contains algebra as a foundation.
According to official calculus prerequisite guidelines, the core requirement is “overall comfort with algebra, geometry, and trigonometry” with specific emphasis on manipulating polynomial expressions, solving equations, and understanding functions. When that comfort is missing, calculus becomes a house built on sand.
To see the full picture, it helps to view all five algebra mistake types side by side in one map.
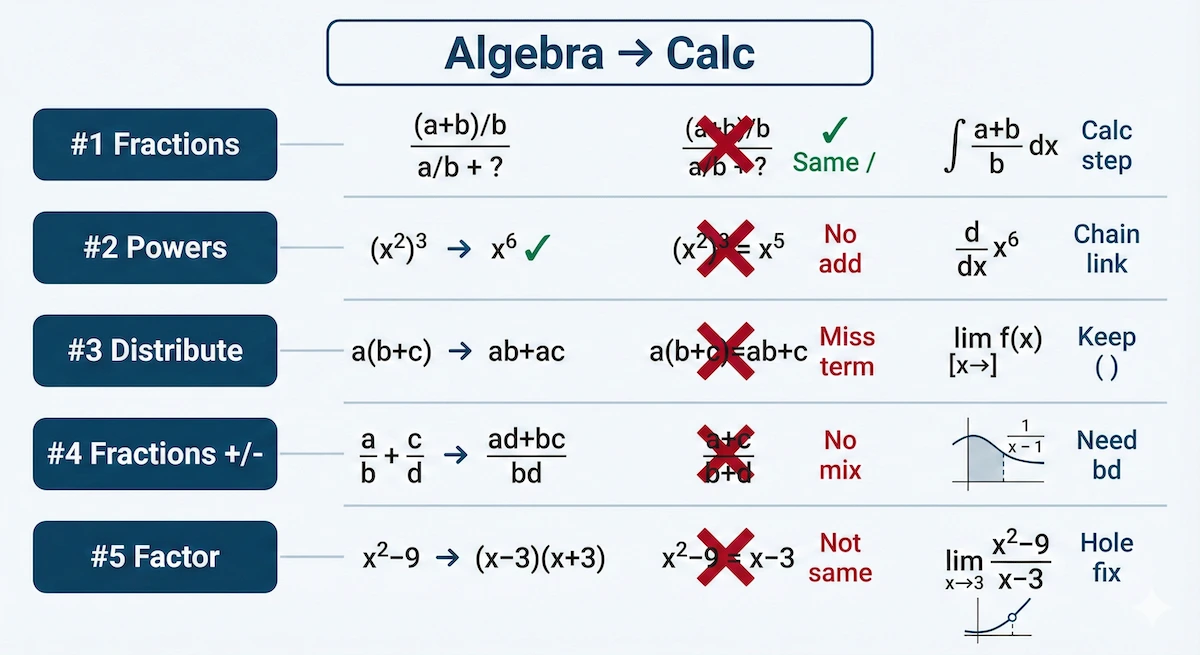
This overview map links each algebra mistake to its calculus impact so you see where to fix first.
Keep this map open as a quick guide while you solve calculus problems so you can spot each error pattern early.
Mistake #1: Incorrectly Canceling Terms (Canceling Addition/Subtraction)
The Error
This is perhaps the most common algebraic mistake that wreaks havoc in calculus. Students see a fraction like (x+2)/(x+4) and believe they can “cancel” the x’s to get 2/4 or simplify it to 1.
WRONG:
(x+2)/(x+4) ≠ 1 + 2/4
Or worse, they see (x²-9)/(x+3) and incorrectly “cancel” the x terms to get (-9)/3.
Why It Happens
Students confuse the rules for canceling. In multiplication and division, you can cancel common factors. For example:
3x/6 = x/2
Here, 3 is a common factor of both numerator and denominator, so cancellation is valid.
But in addition and subtraction, x and 2 in the expression x+2 are terms, not factors. They are being added, not multiplied, so they cannot be canceled.
How to Fix It: The Factor-First Rule
Always factor before canceling. If you see (x²-9)/(x+3), recognize that the numerator is a difference of squares:
x² – 9 = (x+3)(x-3)
Now the fraction becomes:
(x+3)(x-3)/(x+3) = x – 3
Here, (x+3) is a common factor in both numerator and denominator, so it can be canceled.
Critical Check: After simplifying, verify there are no restrictions. In the original expression (x²-9)/(x+3), the denominator x+3=0 when x=-3, so we must note: x ≠ -3.
Impact on Calculus
In calculus, this mistake appears constantly:
• When taking limits: lim(x→2) (x²-4)/(x-2) requires factoring, not canceling terms
Whenever a limit gives 0/0, this is the standard factor–cancel–limit pattern you should fall back on

use this chain when a limit gives 0/0 so you know exactly how to factor and fix it.
Once this chain feels automatic, many “scary” limit questions turn into one or two lines of clean algebra.
• When simplifying derivatives: Many derivative problems require reducing fractions after applying quotient rule
• When solving integration problems: u-substitution often leaves you with fractions requiring simplification
Example Calculus Problem: If you need to simplify (2x² + 3x)/x, correctly you factor:
x(2x+3)/x = 2x + 3
If you incorrectly “cancel terms,” you might get (2+3)/1 = 5, which is nonsensical and breaks your entire problem.
Mistake #2: Misunderstanding and Misapplying Exponent Rules
The Error
Three exponent mistakes plague calculus students:
Mistake 2a: Multiplying the base and exponent
3⁴ ≠ 12 (correct: 3⁴ = 81)
Mistake 2b: Adding exponents when combining like terms
3x² + 4x² ≠ 7x⁴ (correct: 3x² + 4x² = 7x²)
Mistake 2c: Not applying exponent rules correctly to powers of powers
(x²)³ ≠ x⁵ (correct: (x²)³ = x⁶)
Why It Happens
Students don’t understand what an exponent represents. An exponent is shorthand for repeated multiplication. For example:
3⁴ = 3 × 3 × 3 × 3 = 81
It’s not 3 × 4. The base and exponent have completely different roles.
Additionally, students confuse the rule for combining like terms (addition/subtraction) with the rule for exponents (multiplication/division).
Read more to get instant, accurate homework help
How to Fix It: The Seven Essential Exponent Laws
According to standard algebra and precalculus curricula, here are the definitive exponent rules:
1. Product of Powers: a^m × a^n = a^(m+n)
Example: 2³ × 2² = 2⁵ = 32
2. Quotient of Powers: a^m ÷ a^n = a^(m-n)
Example: x⁵ ÷ x² = x³
3. Power of a Power: (a^m)^n = a^(mn)
Example: (x²)³ = x⁶
4. Power of a Product: (ab)^m = a^m × b^m
Example: (2x)³ = 8x³
5. Power of a Quotient: (a/b)^m = a^m/b^m
Example: (x/2)² = x²/4
6. Zero Exponent: a⁰ = 1 (a ≠ 0)
Example: 7⁰ = 1
7. Negative Exponent: a^(-m) = 1/a^m
Example: x^(-3) = 1/x³
Key point for combining like terms: When you add or subtract terms, the exponents stay the same. The only time you add or multiply exponents is when multiplying or raising to a power.
Impact on Calculus
Exponent errors compound dramatically:
• Power rule for derivatives: d/dx(x^n) = nx^(n-1) requires exponent manipulation
• Chain rule applications often involve fractional exponents: d/dx(√x) = d/dx(x^(1/2)) = (1/2)x^(-1/2)
• Integration uses negative exponents: ∫x^(-2) dx = -x^(-1) + C = -1/x + C
Example: If you need to find d/dx(x⁵) and incorrectly add exponents in your work, you’ll get the wrong derivative.
Mistake #3: Not Distributing Properly (FOIL and Distributive Property)
The Error
The distributive property states: a(b+c) = ab + ac
When students expand (x+2)², many make this critical error:
(x+2)² ≠ x² + 4 (WRONG!)
Or they expand (x+2)(x+3) as:
(x+2)(x+3) ≠ x² + 6 (WRONG!)
The correct expansions are:
(x+2)² = (x+2)(x+2) = x² + 2x + 2x + 4 = x² + 4x + 4
(x+2)(x+3) = x² + 3x + 2x + 6 = x² + 5x + 6
Why It Happens
The FOIL method (First, Outer, Inner, Last) is often taught mechanically without students understanding what’s actually happening. They see two binomials and rush through, forgetting that each term in the first binomial must multiply with each term in the second binomial all four combinations must be included and added together.
How to Fix It: The Systematic Method
For any product like (a+b)(c+d), use the box method or systematic distribution:
(a+b)(c+d) = ac + ad + bc + bd
Ensure you have four terms (two binomials = 2 × 2 = 4 terms). After combining like terms, you typically get three terms.
For perfect squares, memorize these critical forms:
(a+b)² = a² + 2ab + b²
(a-b)² = a² – 2ab + b²
(a+b)(a-b) = a² – b²
Example Verification:
(x+3)² = x² + 2(x)(3) + 3² = x² + 6x + 9
Impact on Calculus
Distribution errors cascade through calculus:
• Product rule: d/dx[f(x)g(x)] = f'(x)g(x) + f(x)g'(x) requires distributing and combining terms
• Integration by parts: ∫u dv = uv – ∫v du involves expansion and collection
• Solving differential equations often requires expanding products
Example: When computing d/dx[(x²+1)(x³-2)] using the product rule, you must correctly distribute and combine like terms or your derivative will be wrong.
Mistake #4: Fraction Manipulation Errors (LCD and Cancellation)
The Error
Error 4a: Skipping the LCD when adding/subtracting fractions
x/3 + 2/5 ≠ (x+2)/8
The correct approach requires finding a common denominator (LCD = 15):
x/3 + 2/5 = 5x/15 + 6/15 = (5x+6)/15
Error 4b: Canceling non-factors
Students see (x+2)/(x+4) and think terms can be canceled (which we addressed in Mistake #1). Or they incorrectly simplify (x+1)/(x+3) to 1⅓ as if the terms were mixed numbers.
Why It Happens
Fraction arithmetic from earlier math is rusty or poorly understood. Students rush through or misremember the least common denominator process.
How to Fix It: Systematic Fraction Rules
For Adding/Subtracting Fractions:
1. Find the LCD (least common denominator)
2. Rewrite each fraction with the LCD as the denominator
3. Add or subtract numerators; keep the denominator unchanged
4. Simplify by canceling common factors
Example:
3/x – 1/(x+2)
LCD is x(x+2). Rewrite:
3(x+2)/(x(x+2)) – x/(x(x+2)) = (3x+6-x)/(x(x+2)) = (2x+6)/(x(x+2))
Factor the numerator:
2(x+3)/(x(x+2))
No further cancellation is possible since no factors are common.
For Multiplying Fractions:
(a/b) × (c/d) = ac/bd
Then factor and cancel common factors.
For Dividing Fractions:
(a/b) ÷ (c/d) = (a/b) × (d/c) = ad/bc
Flip the second fraction, then multiply.
When a problem is full of fractions, use a fixed routine so you never “wing it” and split things the wrong way.
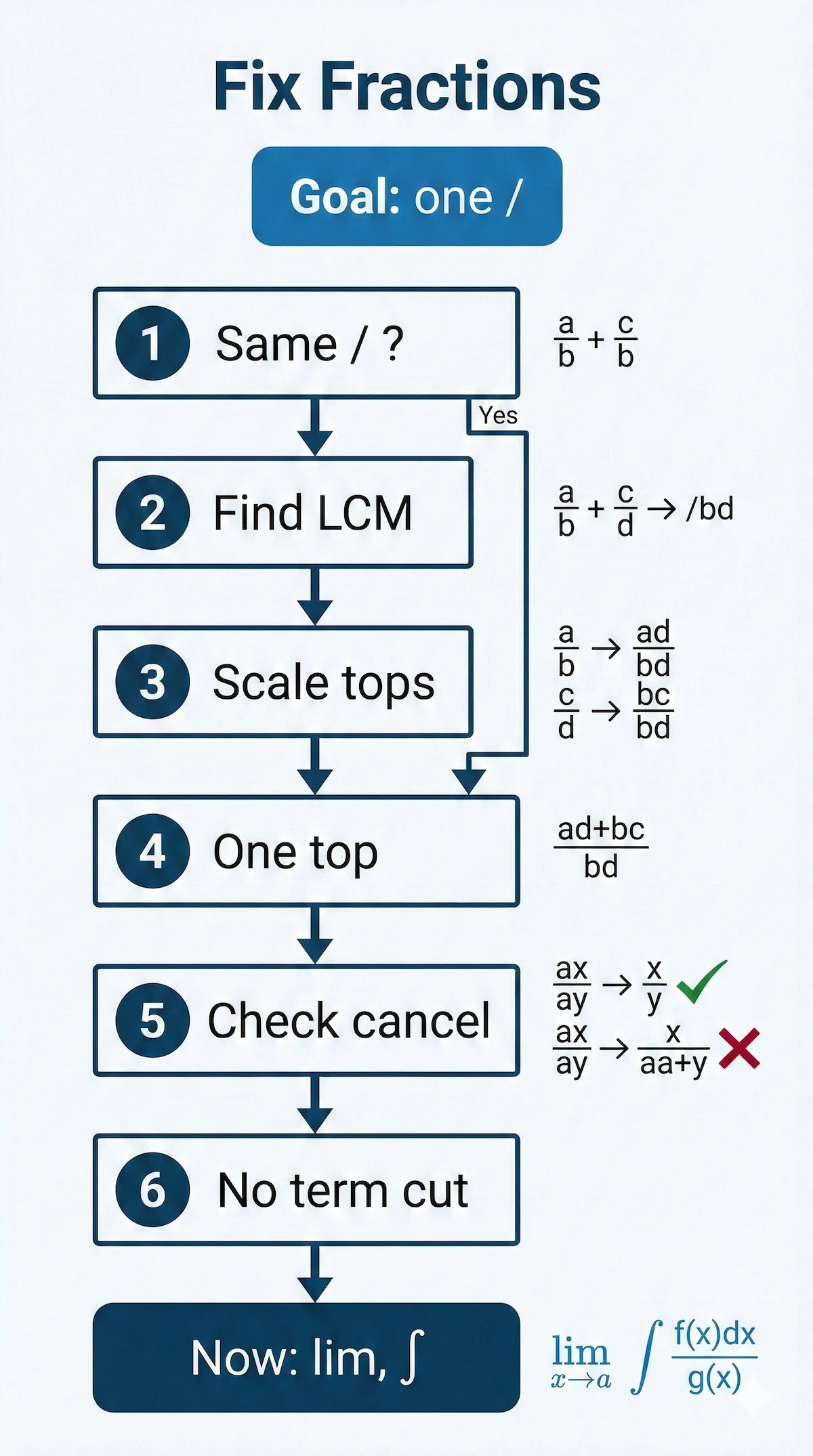
Follow this fraction flow to clean up algebra before you take limits or integrals in calculus.
Run each messy expression through this quick fraction flow before you even think about touching the calculus step.
Impact on Calculus
Fraction errors derail:
• Quotient rule: d/dx[f(x)/g(x)] = (f'(x)g(x) – f(x)g'(x))/[g(x)]² requires fraction manipulation
• Partial fraction decomposition in integration requires adding fractions backward
• Limits often simplify using fraction reduction
Check out smart test prep solutions to score higher
Mistake #5: Factoring Mistakes (Missing GCF, Incomplete Factoring)
The Error
Error 5a: Forgetting to check for GCF first
3x² + 6x = 3x(x + 2) NOT just (x + 2) or left unfactored
Error 5b: Misidentifying factor pairs in quadratic factoring
For x² + 5x + 6, you need two numbers that multiply to 6 AND add to 5:
• 2 × 3 = 6 ✓ and 2 + 3 = 5 ✓
So: x² + 5x + 6 = (x+2)(x+3)
But if a student picks the wrong factors (say, 1 and 6), they get wrong groupings.
Error 5c: Leaving polynomials only partially factored
2x² – 8 = 2(x² – 4) but must continue: 2(x-2)(x+2)
Why It Happens
Students rush and don’t follow a systematic process. Factoring requires careful number sense and pattern recognition, which students skip under time pressure.
How to Fix It: The Factoring Ladder
Apply these methods in order:
Step 1: GCF (Greatest Common Factor)
Factor out any common terms from all parts.
12x³ + 8x² = 4x²(3x + 2)
Step 2: Special Products
• Difference of squares: a² – b² = (a-b)(a+b)
• Perfect square trinomials: a² + 2ab + b² = (a+b)²
• Difference of cubes: a³ – b³ = (a-b)(a²+ab+b²)
Step 3: Quadratic Trinomials (if coefficient of x² is 1)
For x² + bx + c, find two numbers that:
• Multiply to give c
• Add to give b
Then: x² + bx + c = (x + m)(x + n) where mn = c and m + n = b
Example: For x² + 7x + 12:
• Need numbers that multiply to 12 and add to 7
• 3 × 4 = 12 and 3 + 4 = 7 ✓
• Factor: (x+3)(x+4)
Step 4: Quadratic Trinomials (if coefficient of x² is not 1)
Use the AC method or factoring by grouping. For 2x² + 5x + 3:
• a = 2, b = 5, c = 3
• ac = 6; find factors of 6 that add to 5: 2 + 3 = 5
• Rewrite: 2x² + 2x + 3x + 3 = 2x(x+1) + 3(x+1) = (2x+3)(x+1)
Verification Rule: Always multiply back to check your factoring.
Impact on Calculus
Factoring is essential for:
• Simplifying derivatives after quotient rule
• Integration using partial fractions
• Solving related rates problems
• Finding critical points and extrema
Example: When finding critical points of f(x) = x³ – 4x:
f'(x) = 3x² – 4
You need to solve 3x² – 4 = 0, which requires isolating and manipulating the equation correctly.
Seeing all five algebra mistakes side by side makes it easier to spot which ones hurt your own calculus work.
Use this as a quick pre-homework checklist so you stop losing calculus marks to simple algebra slips
Common Mistakes Across All Five: Lack of Verification
A meta-error that compounds all five: students don’t verify their work.
For every algebraic simplification, ask yourself:
1. Did I apply the rule correctly?
2. Can I expand/multiply back to check?
3. Do the units/dimensions make sense?
4. Are there domain restrictions (values that make denominators zero)?
Actionable Study Plan to Fix These Mistakes
Week 1-2: Diagnostic & Assessment
- Take a free algebra diagnostic test from Khan Academy or equivalent resource
• Identify which of the five mistake categories most affect your work
• Focus your effort on the 2-3 weakest areas first
Week 2-3: Focused Remediation
- For each weak area, work through 10-15 practice problems with complete step-by-step solutions
• Use authoritative resources with video explanations
• Do not move on until you score 90%+ on practice problems
Week 3-4: Integration with Calculus
- Start working calculus problems and stop to identify any algebra errors
• When stuck, isolate the algebra step causing the problem
• Return to algebra resources to reinforce that specific skill
• Build a personal “Algebra Error Log” of mistakes you makereview before exams
Ongoing: Prevention
- Always verify work by multiplying out or substituting back
• Write out all steps; don’t skip “obvious” moves
• Check answers using alternative methods when possible
Key Takeaways for Calculus Success
- Algebra is the foundation — No amount of calculus understanding compensates for algebra gaps. Fix the algebra first.2. The five mistakes are fixable — Fraction cancellation, exponent rules, distribution, fraction arithmetic, and factoring are learnable skills with clear procedures.3. Systematic methods beat memorization — Use the ladder approach, the box method, factor-first rule, and LCD method. These prevent errors far better than memorizing disconnected facts.4. Verification is non-negotiable — Always multiply back, check domains, and substitute test values. Catching errors early prevents them from cascading through an exam.5. Early intervention saves your grade — Identify and remediate algebra weaknesses before calculus starts or in the first two weeks of the course. Waiting until midterms makes recovery much harder.
Verified Sources & Resources
These authoritative references validate every claim in this article:
[1] Prior Knowledge & Algebra Error Impact
→ Digital Commons at Utah State University
📖 “The impact of prior knowledge on students’ errors in calculus”
🔗 https://digitalcommons.usu.edu
Research documenting that prerequisite algebra skills directly impact calculus success rates, with 50%+ of errors traceable to algebraic misconceptions rather than calculus concepts.
[2] Algebra as Calculus Foundation
→ Story of Mathematics
📖 “Prerequisites for Calculus – Essential Skills and Knowledge”
🔗 https://storyofmathematics.com
Comprehensive guide establishing algebra manipulation as the foundational skill for calculus proficiency across all topic areas (derivatives, integrals, optimization).
[3] Official Calculus Prerequisites (Most Trusted Resource)
→ Khan Academy
📖 “What to know before taking Calculus”
🔗 https://khanacademy.org
The official, most-trusted educational curriculum guide in North America specifying exact algebra competencies required polynomial manipulation, exponent properties, function representations, solving equations.
[4] Algebraic Fraction Simplification & Domain Restrictions
→ Third Space Learning
📖 “Simplifying Algebraic Fractions”
🔗 https://thirdspacelearning.com
Technical resource on proper factoring procedures before cancellation and domain restriction procedures (identifying values that make denominators zero).
[5] Laws of Exponents (Authoritative Reference)
→ Cuemath
📖 “Laws of Exponents | Exponent Rules Chart”
🔗 https://cuemath.com
Verified chart of all seven exponent rules used in standard algebra and precalculus curricula, establishing the correct formulas for product rule, quotient rule, power of a power, and more.
******************************
This article provides general educational guidance only. It is NOT official exam policy, professional academic advice, or guaranteed results. Always verify information with your school, official exam boards (College Board, Cambridge, IB), or qualified professionals before making decisions. Read Full Policies & Disclaimer , Contact Us To Report An Error

