Cambridge A Level Further Maths (9231) is widely considered the “final boss” of high school mathematics. Since the syllabus overhaul in 2020, students have faced a unique crisis: a lack of relevant past papers.
If you are struggling to find questions that match the new format, or if Further Mechanics is “frying your brain,” you are not alone. Top students don’t just rely on the limited 2020-2024 paper bank; they use specific resource hacks and rigid protocols to minimize error.
Here are 5 Reddit-validated strategies to master the 9231 syllabus.
Need expert learning support? Check out our online tutoring
-
The “Legacy Mine” Strategy (Solving the Resource Shortage)
The biggest pain point for 9231 students is the lack of past papers for the new syllabus (post-2020). “Further Mechanics” (Paper 3) is particularly scarce.
The Fix:
Do not blindly do pre-2020 Further Maths papers—the syllabus was completely different. Instead, mine the Old A Level Maths (9709) archive.
- For Further Mechanics (Paper 3): Use Old 9709 Mechanics 2 (M2) papers from 2010–2019. The content (Projectiles, Moments, Circular Motion) overlaps significantly with the new Further Mechanics syllabus.
Since relevant papers are scarce, you need to know exactly where to look in the archives. This map shows which specific ‘Old Syllabus’ papers correspond to your new exam requirements:
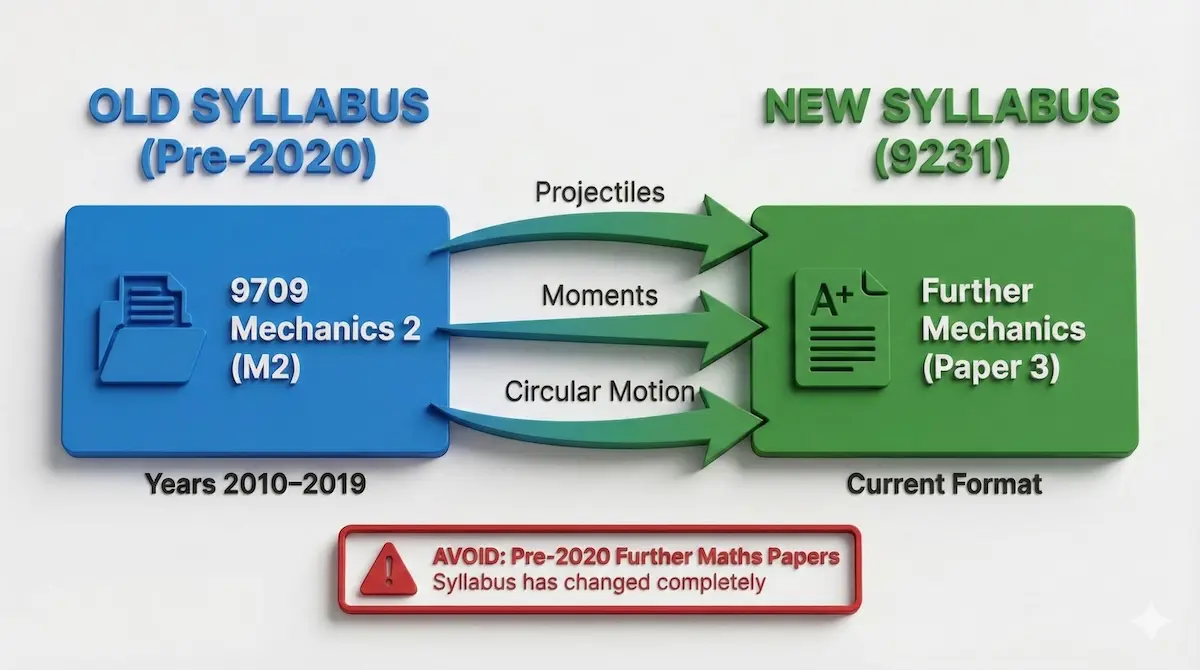
Don’t run out of practice questions—use this map to find relevant problems in the old 9709 archive.
By sticking to these specific years and topics, you get high-quality practice without wasting time on irrelevant material.
- Why it works: You get 10+ years of high-quality, relevant practice questions that are almost identical in style to your exam, without wasting time on removed topics.
-
The “Polar Table” Protocol (For FP1 Integration)
“Finding the limits of integration” for Polar Coordinates is consistently cited as a “brain fryer.” Students often guess the limits based on a rough sketch and lose all accuracy marks.
The Fix:
Stop “eyeballing” the graph. Use the Table Method before you integrate.
- Sketch: Draw the rough shape (e.g., cardioid).
- Table: Create a quick table for $\theta = 0, \pi/2, \pi, 3\pi/2$. Calculate $r$ for each.
- Verify: Check where $r < 0$ (if the loop exists).
- Integrate: Set your limits strictly based on the table values where the curve closes or intersects.
Visualizing the integration limits is difficult, so rely on a structured process instead of guesswork. Follow this exact protocol for every polar question:
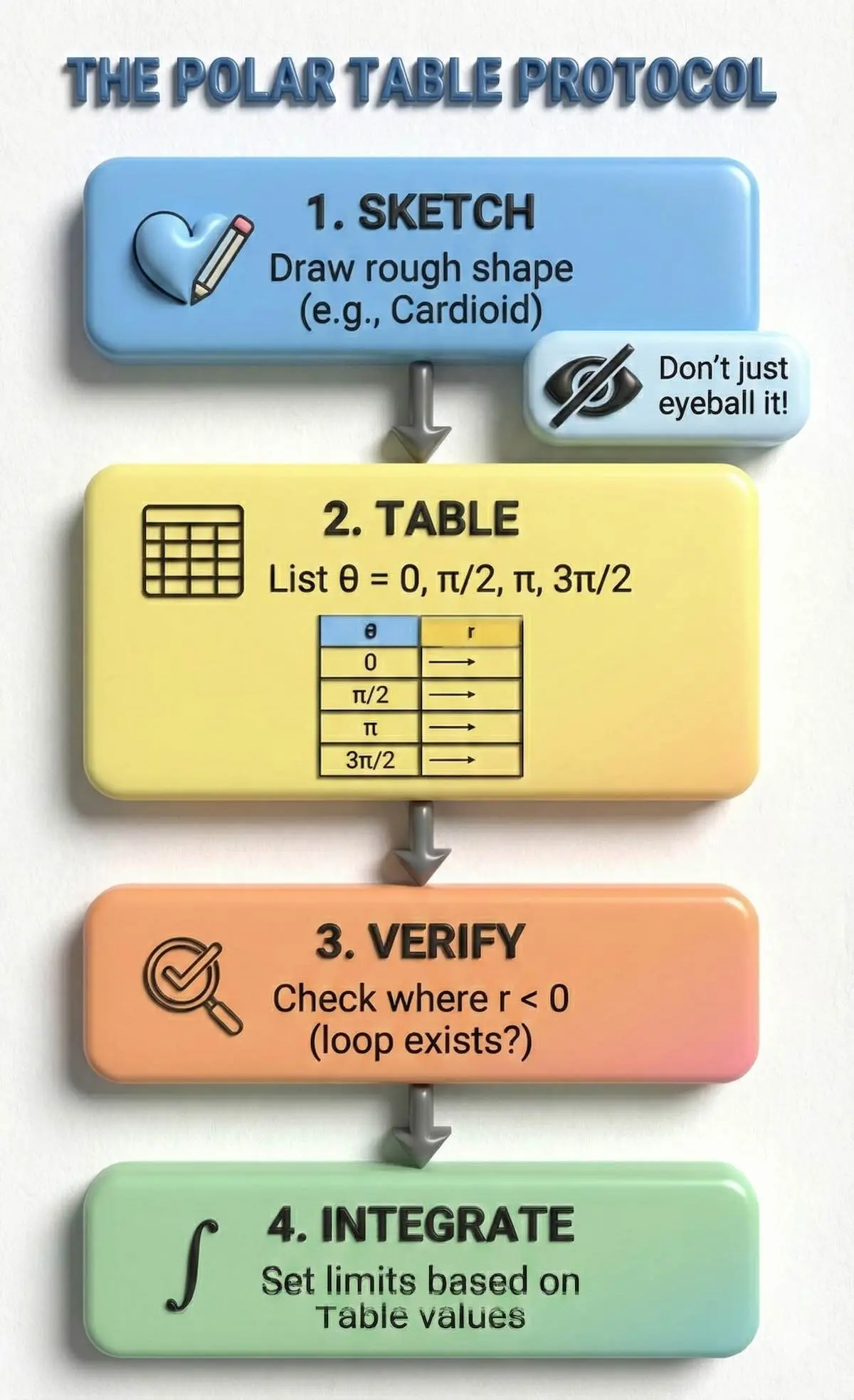
Stop guessing your limits of integration—follow this 4-step protocol to guarantee accuracy in FP1 questions.
This table method ensures you never integrate over a ‘ghost loop’ that doesn’t exist mathematically.
Why it works:
It forces you to mathematically verify where the loop starts and ends, preventing the common mistake of integrating over a region where the curve doesn’t exist.
-
The “Matrix Algorithm” (Protection Against Sign Errors)
In Further Pure 2, diagonalizing a matrix ($P^{-1}AP = D$) is a minefield. One dropped negative sign in step 1 ruins the entire 10-mark question.
The Fix:
Treat Matrix questions as a Computer Algorithm, not math.
- Step 1: Calculate Eigenvalues ($\lambda$). Check: Do they sum to the Trace of A?
- Step 2: Calculate Eigenvectors. Check: Is $Av = \lambda v$ for one simple vector?
- Step 3: Form $P$ and $D$.
- Step 4: Stop. Do not calculate $P^{-1}$ unless explicitly asked.
Why it works:
The “Trace Check” (Step 1) takes 5 seconds. If the sum of your $\lambda$s doesn’t equal the sum of the main diagonal, you know you made a mistake immediately, saving you 15 minutes of wasted work.
Matrix questions are prone to simple sign errors that cost easy marks. Use this algorithmic approach to catch mistakes instantly:
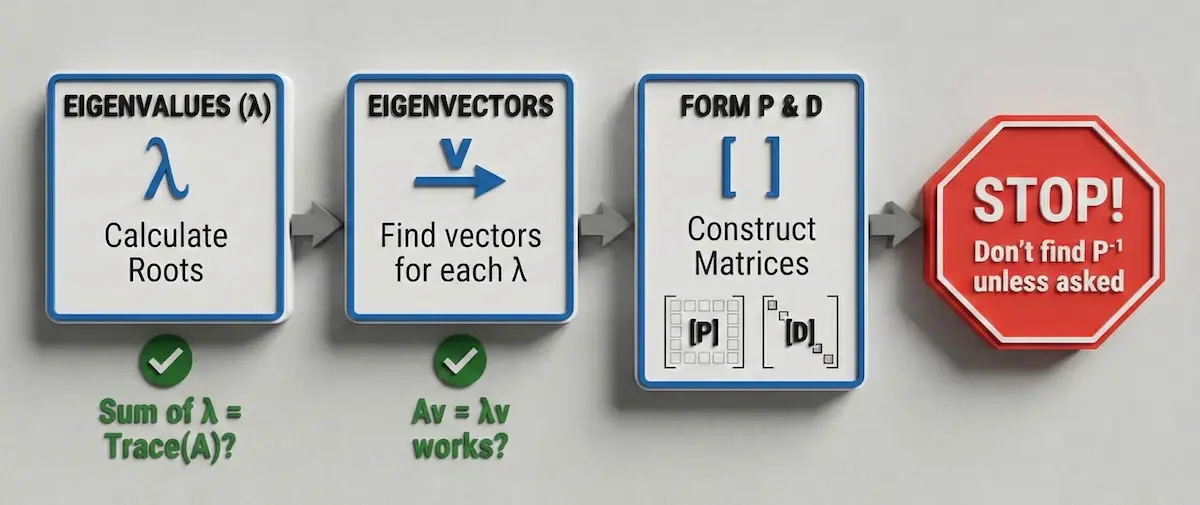
Treat matrix questions like a computer algorithm with these built-in sanity checks to prevent sign errors.
The ‘Trace Check’ in step 1 is the most valuable 5 seconds you will spend in the exam hall.
Read more to get instant, accurate homework help
-
Dimensional Analysis “Sanity Checks” (Further Mechanics)
Further Mechanics problems (like Variable Force or Circular Motion) often result in complex algebraic expressions. Unlike Pure Maths, you can’t always “see” if the answer looks right.
The Fix:
Use Dimensional Analysis to verify every derived formula.
- If you derived an expression for Tension ($T$), the units must reduce to Newtons ($kg \cdot m/s^2$).
- If your answer is $T = \frac{mv}{r}$, the units are $\frac{kg \cdot (m/s)}{m} = \frac{kg}{s}$, which is wrong. You missed a squared term ($v^2$).
Why it works:
This is the single fastest way to catch algebraic derivation errors in Paper 3 without looking at the mark scheme.
-
The “Energy vs. Force” Decision Tree
In Vertical Circular Motion, students often lose marks by using the wrong principle. Using $F=ma$ when you should have used Energy Conservation (or vice versa) is a common trap.
The Fix:
Memorize this decision tree:
- Speed/Velocity required? $\rightarrow$ Conservation of Energy. (Energy doesn’t care about direction, just height).
- Tension/Reaction Force required? $\rightarrow$ Equation of Motion ($F=ma$). (Forces are vectors and depend on position).
- “Slacking” strings? $\rightarrow$ Find where Tension = 0.
- Leaving the surface? $\rightarrow$ Find where Reaction (R) = 0.
Confusion between Energy methods and Force methods is the #1 reason students lose marks in Mechanics. Memorize this decision tree to make the right choice every time:
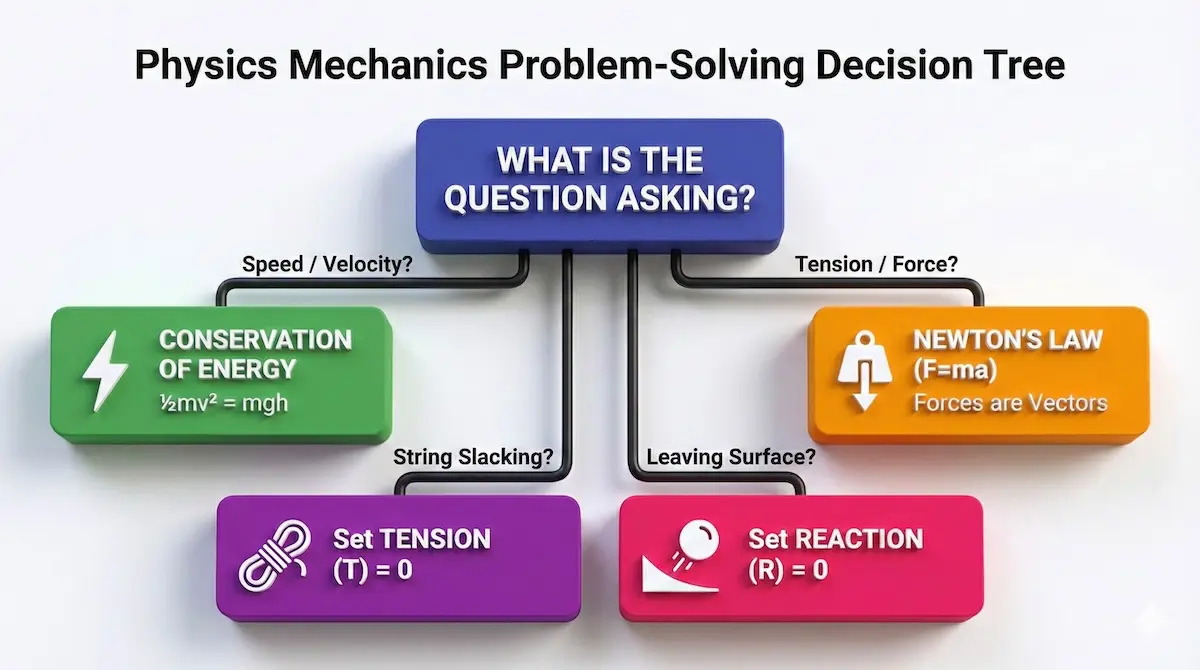
Memorize this decision tree to instantly know whether to use Energy Conservation or Newton’s Laws in exam questions.
When you let the variable dictate the method, you eliminate the panic of not knowing how to start.
Why it works:
It removes the guesswork. You stop asking “how do I start?” and immediately pick the right tool for the specific variable asked.
Check out smart test prep solutions to score higher
How to Apply These Strategies
Here’s a simple weekly routine you can follow:
Monday: Topic review + basic exercises
Tuesday: Past paper practice (timed)
Wednesday: Mistake log review + topic drill
Thursday: Group study / tutor support session if available
Friday: Full paper simulation
Weekend: Big review session + recap weaker sections
This balance keeps you moving forward without burning out.
Consistency beats intensity when studying for Further Maths. Here is a visual breakdown of how a successful week should look:
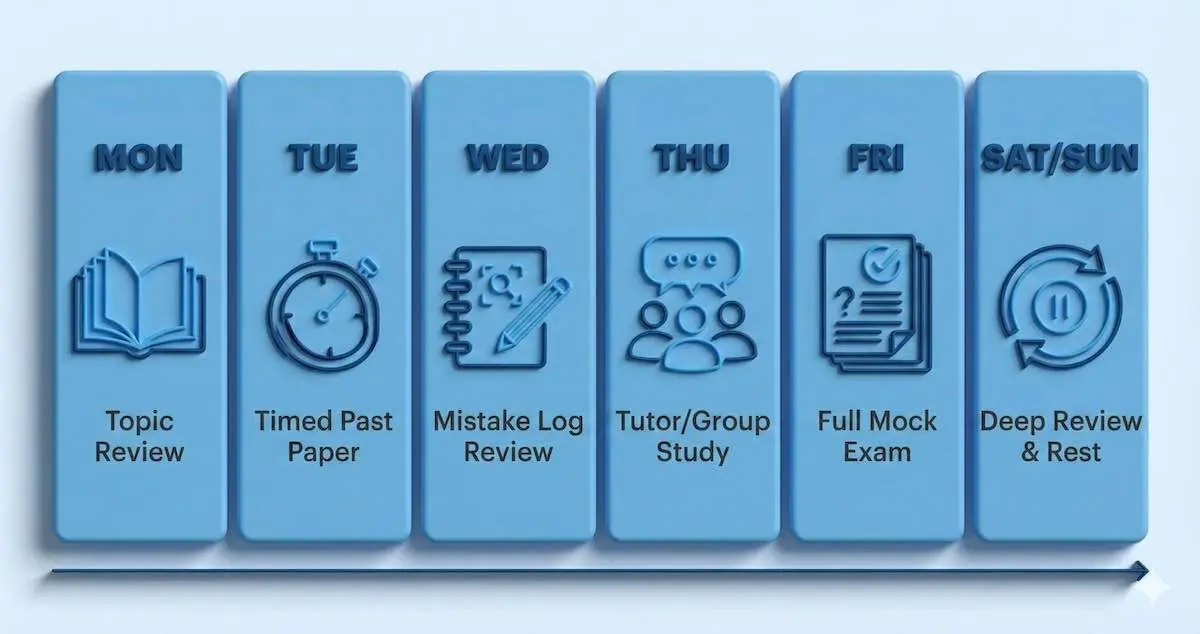
A balanced weekly routine that mixes topic drills, timed practice, and mistake review is key to consistent progress.
Notice how ‘Mistake Log Review’ is treated as a separate study session—this is where the real grade improvement happens.
Key Takeaways
1.Break the syllabus into topics and master them one at a time.
2. Use a structured and consistent revision schedule.
3. Past papers and mark schemes are essential practise regularly.
4. Use authoritative textbooks and online resources to fill gaps.
5. Review mistakes meaningfully and teach concepts you struggle with.
Conclusion
A Level Further Maths (9231) is demanding, but with the right study strategies, you can approach it with confidence. Organised planning, consistent practice, topic mastery, and careful review make all the difference. Use these five proven strategies to make your revision effective and strategic rather than just hard. After reading this article, you’ll have a clear plan to prepare More deeply, manage your study time better, and understand exactly how to tackle advanced Further Maths problems in exams.
******************************
This article provides general educational guidance only. It is NOT official exam policy, professional academic advice, or guaranteed results. Always verify information with your school, official exam boards (College Board, Cambridge, IB), or qualified professionals before making decisions. Read Full Policies & Disclaimer , Contact Us To Report An Error

