Kinematics equations

What is kinematics

Before we study kinematics equations, it is a good idea to understand what Kinematics is.

When we observe nature, we see many objects in motion. From experience, we recognize that motion represents the continuous change in the position of an object with time. We study dynamics in two parts kinematics & kinetics. In kinematics, we study motion in terms of space and time without knowing the cause of motion (the forces that caused the motion). In kinetics, we are also concerned about the cause of motion (forces).

(If you want private 1:1 online tutoring or homework help from an experienced physics tutor at an affordable rate, feel free to WhatsApp us. We will get you started right away).

Kinematic equations list

${v_x} = {v_{ox}} + {a_x}t$ …(1)

$x = {x_0} + {v_{ox}}t + \frac{1}{2}{a_x}{t^2}$ …(2)

$v_x^2 = v_{ox}^2 + 2{a_x}(x - {x_0})$ …(3)

$(x - {x_0}) = \frac{1}{2}\left( {{v_{ox}} + {v_x}} \right)t$ …(4)

Equations (1), (2) & (3) (and sometimes (4)) are the equations of motion with constant acceleration. These are also known as equations of kinematics or kinematic equations.

${v_x}:$ velocity of particle along x-axis of time t

${v_{ox}}:$ velocity of particle along x-axis at t = 0

${a_x}:$ constant acceleration of particle along x-axis

x: position of the particle at time t on the x-axis

${x_o}:$ position of particle at time t = 0 on the x-axis

t: it represents general time.

How to use kinematic equations

The kinematic equation for time, the kinematic equation for velocity

we have first equation of kinematics ${v_x} = {v_{ox}} + {a_x}t$

This expression enables us to determine the velocity at any time t if the initial velocity, the acceleration, and the elapsed time are given.

We have second equation of kinematics $x = {x_o} + {v_{ox}}t + \frac{1}{2}{a_x}{t^2}$ .

This expression enables us to determine the distance traveled during any time t if the initial velocity, acceleration, and time elapsed are known.

We have a third equation that lets us determine the final velocity if the initial velocity, acceleration, and displacement are known.

Solved problems on each kinematic equation

Example 1

An athlete takes 20 sec to reach his maximum speed of 18.0 km/h. What is the magnitude of average acceleration?

Ans. Her athlete is running along the x-axis with constant acceleration; we can use

${v_x} = {v_{ox}} + {a_x}t$

$18 \times \frac{5}{{18}}{\rm{m/s}} = 0 + {a_x} \times 2\,\sec$

$5\,{\rm{m/s}} = {a_x} \times 2\,\sec$

${a_x} = 2.5\,{\rm{m/}}{{\rm{s}}^{\rm{2}}}$

Therefore, the magnitude of the average acceleration is 2.5 m/s².

Example 2

An object having a velocity of 4.0 m/s is accelerated at the rate of 1.2 m/s² for 5.0 sec. Find the distance traveled during the period of acceleration.

Ans. Suppose the object is moving along the +ve x-axis.

Assuming that the initial location of the particle is at the origin.

Here, $x - {x_o} = x - 0 = x$

${v_{ox}} = 4.0\,{\rm{m/s}}$ , ${a_x} = 1.2\,{\rm{m/}}{{\rm{s}}^2}$ , $t = 5\,\sec$ .

Using kinematics equation,

$x = {x_o} + {v_{ox}}t + \frac{1}{2}{a_x}{t^2}$

$\Rightarrow x - {x_o} = {v_{ox}}t + \frac{1}{2}{a_x}{t^2}$

$\Rightarrow x = \left[ {4 \times 5 + \frac{1}{2} \times 1.2 \times {{(5)}^2}} \right]meter$

$\Rightarrow x = \left[ {20 + \frac{{1.2}}{2} \times 25} \right]meter$

$\Rightarrow x = 35\,meter$

Example 3

A person traveling at 43.2 km/h applies the brake giving a deceleration of 6.0 m/s² to his scooter. How far will it travel before stopping?

Ans. Suppose the person is traveling along the positive x-axis and initially that person was at the origin (x = 0).

He is moving along a straight line with constant negative acceleration.

Using kinematics equation,

$v_x^2 = v_{ox}^2 + 2{a_x}(x - {x_o})$

Here, ${v_x} = 0\,;\,\,{v_{ox}} = 12\,{\rm{m/s}}\,;\,\,{a_x} = - \,6.0\,{\rm{m/}}{{\rm{s}}^{\rm{2}}};\,\,(x - {x_o}) = ?$

$\Rightarrow \quad {0^2} = {(12\,{\rm{m/s}})^2} + 2( - \,6\,{\rm{m/}}{{\rm{s}}^{\rm{2}}})(x)$ [because $x - {x_o} = x - 0 = x$ ]

$\Rightarrow \quad 12x = 144$

$\Rightarrow \quad x = 12\,m$

So, the person will travel a distance of 12 m before stopping.

The kinematic equations for projectile motion

The projectile’s motion can be discussed separately for the horizontal and vertical parts. We take origin $({x_o} = 0,\,\,{y_o} = 0)$ at the point of projection. The instant when the particle was projected is taken as t = 0. The plane of motion is taken as the x-y plane, the horizontal line OX as the x-axis and the vertical line OY as the y-axis. Vertically upward direction is taken as the positive direction of the y-axis.

We have, ${v_{ox}} = {v_o}\cos {\alpha _o}\,;\,\,{a_x} = 0$

${v_{oy}} = {v_o}\sin {\alpha _o}\,;\,\,{a_y} = - g$

Horizontal motion

${a_x} = 0$ , we have

${v_x} = {v_{ox}} + {a_x}t$

$\Rightarrow \quad {v_x} = {v_{ox}}$

Again, $x - {x_0} = {v_{ox}}t + \frac{1}{2}{a_x}{t^2}$ [Here, ${a_x} = 0\,;\,\,{v_{ox}} = {v_o}\sin {\alpha _o}\,;\,\,{x_o} = 0$ ]

$\Rightarrow \quad x - {x_0} = {v_{ox}}t$

$\Rightarrow \quad x = {x_0} + {v_{ox}}t$

Vertical Motion

The acceleration of the particle is g in the downward direction.

Thus ${a_y} = - g$ [Here, ${a_y} = - g\,;\,\,{v_{oy}} = {v_o}\sin {\alpha _o}\,;\,\,{y_o} = 0$ ]

We can write, ${v_y} = {v_{oy}} + {a_y}t$

$\Rightarrow {v_y} = {v_{oy}} - gt$

and $y - {y_o} = {v_{oy}}t + \frac{1}{2}{a_y}{t^2}$

$\Rightarrow y = {y_o} + {v_{oy}}t + \frac{1}{2}{a_y}{t^2}$

Again, $v_y^2 = v_{oy}^2 + 2{a_y}(y - {y_o})$

Kinematic equations for free-fall

A typical example of motion in a straight line with constant acceleration is the free fall of a body near the earth’s surface.

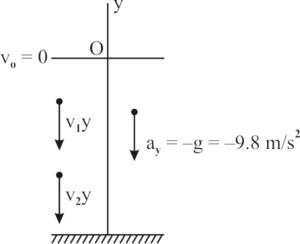
Here, we have taken the origin O at the starting point and the upward direction as positive. Assuming the initial portion co-ordinate ${y_o}$ and initial velocity is ${v_{oy}}$ .

The y-acceleration is downward (i.e., along the –ve y-direction) therefore, ${a_y} = - g$ .

After time t, its position co-ordinate can be written as

$y - {y_o} = {v_{oy}}t + \frac{1}{2}{a_y}{t^2}$

$\Rightarrow y = {y_o} + {v_{oy}}t + \frac{1}{2}( - g){t^2}$

Here in this case, ${y_o} = 0\,;\,\,{v_{oy}} = 0$

After time t, its velocity co-ordinate ${v_y} = {v_{oy}} + {a_y}t$

$\Rightarrow {v_y} = {v_{oy}} - gt$

Here ${v_{oy}} = 0{\rm{ and }}{a_y} = - \,g$

We can also write, $v_y^2 = v_{oy}^2 + 2{a_y}(y - {y_o})$

$\Rightarrow v_y^2 = v_{oy}^2 + 2( - g)(y - {y_o})$

Here, ${a_y} = - \,g{\rm{ and }}{y_o} = 0$

Kinematic equations for rotation

When a body revolves about a stationary axis (usually z-axis), the position of the body is described by an angular position coordinate $\theta$ . If the angular acceleration is constant, then $\theta$ , ${\omega _2}$ and ${\alpha _2}$ are related by simple kinematic equations.

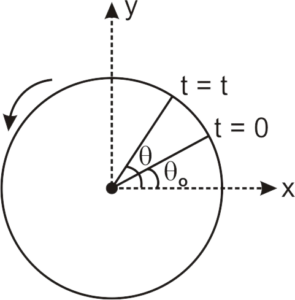
Kinematic equations in the case of rotation are as follows:

$\theta - {\theta _o} = {\omega _{oz}} + \frac{1}{2}{\alpha _z}{t^2}$

$\Rightarrow {\omega _z} = {\omega _{oz}} + {\alpha _z}t$

$\Rightarrow \omega _z^2 = \omega _{oz}^2 + 2{\alpha _z}(\theta - {\theta _o})$

Here, ${\theta _o}:$ Angular position of the body at time t = 0

$\theta:$ Angular position of the body at time t = t

${\alpha _z}:$ Constant angular acceleration of the body

${\omega _{oz}}:$ Angular velocity of the body at time t = 0

${\omega _z}:$ Angular velocity of the body at time t = t

Kinematic equation derivation using calculus

Let a particle is moving along x-axis. Initially assuming particle was at $x = {x_o}$ and particle has initial velocity ${v_{ox}}$ .

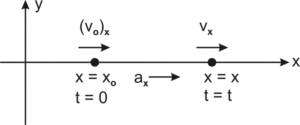
The particle has a constant acceleration along the x-axis. ${a_x}$ from the definition of acceleration.

${a_x} = \frac{{d{v_x}}}{{dt}}\quad \Rightarrow \quad d{v_x} = {a_x}dt$

Integrating both sides with proper limits

$\int\limits_{{v_{ox}}}^{{v_x}} {d{v_x}} = \int\limits_o^t {{a_x}} \,dt$

$\Rightarrow {v_x} - {v_{ox}} = {a_x}(t - 0)$

$\Rightarrow \quad {v_x} = {v_{ox}} + {a_x}t$

Again from the definition of velocity

${v_x} = \frac{{dx}}{{dt}} \Rightarrow \frac{{dx}}{{dt}} = {v_{ox}} + {a_x}t$

$\Rightarrow dx = ({v_{ox}} + {a_x}t)\,dt$

Now, integrating both sides with proper limits

$\int\limits_{{x_o}}^x {dx} = \int\limits_0^t {({v_{ox}} + {a_x}t)\,dt}$

$\Rightarrow x - {x_o} = {v_{ox}}(t - 0) + {a_x}\left[ {\frac{{{t^2}}}{2}} \right]_0^t$

$\Rightarrow \quad x - {x_o} = {v_{ox}}t + \frac{1}{2}{a_x}{t^2}$

Again starting from, ${a_x} = \frac{{d{v_x}}}{{dt}}$

$\frac{{d{v_x}}}{{dx}} \cdot \frac{{dx}}{{dt}} = {a_x} \Rightarrow {v_x} \cdot \frac{{d{v_x}}}{{dt}} = {a_x}$

$\Rightarrow {v_x} \cdot d{v_x} = {a_x}(dx)$

Now, integrating both sides,

$\int\limits_{{v_{ox}}}^{{v_x}} {{v_x}dx} = \int\limits_{{x_o}}^x {{a_x}(dx)} \Rightarrow \left[ {\frac{{v_x^2}}{2}} \right]_{{v_{ox}}}^{{v_x}} = {a_x}(x - {x_o})$

$\Rightarrow \quad v_x^2 = v_{ox}^2 + 2ax(x - {x_o})$

Example

A particle starts with an initial velocity of 2.5 m/s along the positive x-direction and accelerates uniformly at the rate of 0.5 m/s². Find the distance traveled by it in the first two seconds.

Ans. Let particle stats its motion from the origin with an initial velocity of

${v_{ox}} = 2.5\,{\rm{m/s}}\,{\rm{;}}\,\,{{\rm{a}}_x} = 0.5\,{\rm{m/}}{{\rm{s}}^2}$

Using, ${a_x} = \frac{{d{v_x}}}{{dt}} \Rightarrow d{v_x} = {a_x}dt$

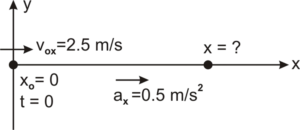
Now, integrating both sides,

$\int\limits_{{v_{ox}}}^{{v_x}} {d{v_x}} = {a_x}\int\limits_0^t {dt}$

$\Rightarrow {v_x} - 2.5 = \frac{1}{2}(t - 0) \Rightarrow {v_x} = 2.5 + \frac{t}{2}$

Again using ${v_x} = \frac{{dx}}{{dt}}$

$\Rightarrow \frac{{dx}}{{dt}} = 2.5 + \frac{t}{2} \Rightarrow dx = \left( {2.5 + \frac{t}{2}} \right)dt$

Now, integrating both sides,

$\int\limits_{{x_o}}^x {dx} = \int\limits_0^2 {\left( {2.5 + \frac{t}{2}} \right)dt}$

$\Rightarrow x - {x_o} = 2.5(2 - 0) + \frac{1}{2}\frac{{{{(2)}^2}}}{2}$

Since the particle does not turn back, the distance traveled equals 6 m.

Kinematics equation for nonuniform acceleration

If the acceleration of a particle during its motion does not remain constant, then both motion and acceleration are nonuniform.

As by definition, ${v_x} = \frac{{dx}}{{dt}}\,\,;\,\,{a_x} = \frac{{{d^2}x}}{{d{t^2}}}$

If x is a function of time, the second derivative of displacement with respect to time represents acceleration.

If velocity is a function of position, then by chain rule of differentiation.

${a_x} = \frac{{d{v_x}}}{{dt}} = \frac{{d{v_x}}}{{dx}} \cdot \frac{{dx}}{{dt}}$

$\Rightarrow {a_x} = v\frac{{d{v_x}}}{{dx}}$

Example

The acceleration ${a_x}$ of a particle moving in a straight line varies with its displacement $x = 2{a_x}$ . The velocity of the particle is zero at zero displacements. Find the corresponding velocity displacement equation.

Ans. We have, ${a_x} = 2x$

$\Rightarrow \frac{{d{v_x}}}{{dx}} \cdot \frac{{dx}}{{dt}} = 2x$

$\Rightarrow {v_x}(d{v_x}) = 2x(dx)$

Now, integrating both sides with proper limits

$\int\limits_o^{{v_x}} {{v_x}(d{v_x})} = \int\limits_o^x {2x(dx)}$

$\Rightarrow \frac{{v_x^2}}{2} = 2 \cdot \frac{{{x^2}}}{2} \Rightarrow v_x^2 = 2{x^2}$

$\Rightarrow \quad {v_x} = \pm \sqrt 2 x$ .

Resources