The Law of Conservation of Angular Momentum

Angular momentum is the moment of linear momentum of a body with respect to an axis of rotation.

Angular momentum of a particle about O is defined as ${bf{L}} = {bf{r}} times {bf{P}}$

For more info, please check Angular Momentum.

The law of conservation of angular momentum

If the total external torque on a system about a particular point equals zero, then the system’s total angular momentum about that particular point will remain conserved.

Proof of the law of conservation of angular momentum

If the total external torque on a system about a particular point equals zero, then the system’s total angular momentum about that particular point will remain conserved.

If ${Gamma _{net}} = frac{{dL}}{{dt}} = 0,;$ then L remains constant or conserved.

As we know, the angular momentum of body is defined as,

$L = sum left( {{r_i} times {P_i}} right)$

Now, differentiating with respect to time,

$frac{{dL}}{{dt}} = frac{d}{{dt}}sum left( {{r_i} times {P_i}} right) = sumlimits_i^{} {left[ {frac{{d{r_i}}}{{dt}} times {P_i} + r times frac{{d{P_i}}}{{dt}}} right]}$

$frac{{dL}}{{dt}} = sumlimits_i^{} {left[ {{v_i} times m{v_i} + {r_i} times {F_i}} right]}$

Here, ${v_i} times m{v_i} = 0$ ,

so, $frac{{dL}}{{dt}} = sumlimits_i^{} {{r_i} times {F_i}} = {Gamma _{total}}$

Here, ${F_i}$ is the total force acting on the i^th particle.

This includes any external force as well as the forces on the i^th particle by all the other particles. Taking summation of both sides, internal torque adds to zero.

$sumlimits_{}^{} {{Gamma ^{ext}}} = frac{{dL}}{{dt}}$

Here, ${Gamma ^{ext}}$ is the total torque due to all the external forces acting on the system.

If the torque of external forces about any particular point is equal to zero, then $frac{{dL}}{{dt}} = 0$ . This means the system’s total angular momentum about that particular point will remain constant.

${left( {sumlimits_{}^{} {{L_{sys,,0}}} } right)_i} = {left( {sumlimits_{}^{} {{L_{sys,,0}}} } right)_f}$ if $Gamma _0^{ext} = 0$ .

Problems based on the angular momentum conservation principle

Question 1: A stationary wheel dropped onto a rotating wheel

A wheel is rotating at an angular $omega$ about its axis, which is kept vertical. An identical wheel initially at rest is gently dropped into the same axle, and the two wheels start rotating with a common angular speed. Find this common angular speed.

Ans.: Let the moment of inertia of the wheel about the axis be I. Initially, the first wheel was rotating at the angular speed $omega$ about the axle, and the second wheel was at rest. Considering both the wheels together as a system. The total angular momentum of the system before the coupling is $(Iomega + 0)$ . Afterward, the second wheel is dropped into the axle, and the two wheels slip on each other and exert forces of friction. These forces of friction have torques about the axes of rotation, but these are torques of internal forces. No external torque is applied to the two-wheel system. Hence total angular momentum of the system remains unchanged. If the common angular speed is $omega '$ , the total angular momentum of the two-wheel system is $2Iomega '$ after the coupling.

Hence, $Iomega = 2Iomega 'quad Rightarrow quad omega ' = frac{omega }{2}$

Problem 2: A boy folds and unfolds his arms while rotating

A boy stands on a freely rotating platform. When he folds his arms, his revolution frequency equals 0.8 rev/s. Now he extends his arms his rotation frequency becomes 0.25 rev/s. Find the ratio of moment of inertia in the first case to that in the second.

Ans.: Let (boy + platform) as a system,

Here, the total angular momentum of the system will be conserved.

$[{I_1}{omega _1}] = [{I_2}{omega _2}]$

$Rightarrow quad {I_1}2pi {v_1} = {I_2}2pi {v_2}$

$Rightarrow quad {I_1} times 0.8,rev{rm{/}}s = {I_2} times 0.25,rev{rm{/}}s$

$Rightarrow quad frac{{{I_1}}}{{{I_2}}} = frac{{0.25}}{{0.8}}quad Rightarrow quad frac{{{I_1}}}{{{I_2}}} = frac{5}{{16}}$

Problem 3: A person jumping on a rotating merry go round

A merry go round of radius 1.5 m and moment of inertia $I = 150,kg{rm{ - }}{{rm{m}}^2}$ is spinning with initial angular speed $omega = 1.5,rad{rm{/s}}$ in clockwise direction when viewed from above. A person with a mass of 50 kg and a velocity of 5 m/s runs on a path tangent to the merry-go-round. Once at the merry-go-round, the person jumps on and holds on to the rim. What is the angular speed of the merry-go-round after the person jumps on?

Note: This problem is left as an exercise. If you are unable to solve it, please contact us on WhatsApp, and one of our Physics tutors will explain this problem in a live, 1:1 private online Physics tutoring session.

Example 4: Sudden contraction of earth and the length of the new day

If the earth were to suddenly contract to $frac{1}{n}$ th of its present radius without any change in its mass, the duration of the new day would be nearly _________.

Ans.- Considering earth as a system;

Since, ${bf{Gamma }}_{cm}^{ext} = 0,;,,{({{bf{L}}_{sys,,cm}})_i} = {({{bf{L}}_{sys,,cm}})_f}$

$Rightarrow quad {({I_{sys,,cm}})_i}{{bf{omega }}_i} = {({I_{sys,,cm}})_f}{{bf{omega }}_f}$

$Rightarrow quad frac{2}{5}mr_i^2{{bf{omega }}_i} = frac{2}{5}mr_f^2{{bf{omega }}_f}$

Taking magnitude both sides,

$Rightarrow quad r_i^2{{bf{omega }}_i} = {left( {frac{{{r_i}}}{n}} right)^2}{{bf{omega }}_f}$

$Rightarrow quad {{bf{omega }}_i} = frac{1}{{{n^2}}}{{bf{omega }}_f}$

$Rightarrow quad {{bf{omega }}_f} = {{bf{omega }}_i}{n^2}$

Again time period of the earth ;

$T = frac{{2pi }}{omega }quad Rightarrow quad T propto frac{1}{omega }$

${T_i}{omega _i} = {T_f}{omega _f}quad Rightarrow quad (24,hr){omega _i} = {T_f}{omega _i}{n^2}$

$Rightarrow quad {T_f} = frac{{(24,hr)}}{{{n^2}}}$ .

Example 5: Kinetic energy and angular momentum of a body in a uniform circular motion

A particle performs uniform circular motion with an angular momentum L. If we double the angular frequency f of the particle and reduce the kinetic energy to half, its angular momentum becomes ________.

Ans.- According to our question, ${(KE)_f} = frac{1}{2}{(KE)_i}$

$Rightarrow quad frac{1}{2}{I_f}omega _f^2 = frac{1}{2} cdot frac{1}{2}{I_i}omega _i^2$

Also, ${omega _f} = 2{omega _i}$ $Rightarrow quad {I_f}{(2{omega _i})^2} = frac{1}{2}{I_i}omega _i^2$

$Rightarrow quad {I_f} cdot 4omega _i^2 = frac{1}{2}{I_i}omega _i^2quad Rightarrow quad 8{I_f} = {I_i}$

Also, from the principle of conservation of angular momentum,

$frac{{{L_i}}}{{{I_i}{omega _i}}} = frac{{{L_f}}}{{{I_f}{omega _f}}} Rightarrow quad {L_f} = frac{{{L_i} times {I_f}{omega _f}}}{{{I_i}{omega _i}}}$

$Rightarrow quad {L_f} = Lfrac{{{I_f}}}{{8{I_f}}}frac{{2{omega _i}}}{{{omega _i}}}quad Rightarrow quad {L_f} = frac{{{L_i}}}{4} = frac{L}{4}$ .

Example 6: Two small masses land on the rim of a rotating ring

A circular ring of mass M is rotating about its axis in a horizontal plane at an angular velocity. If two point size bodies, each of mass m, are gently attached to the rim of the ring at two ends of its diameter, then the angular velocity of the ring is _________.

Ans.-

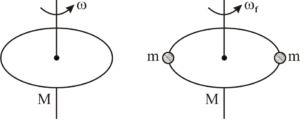
Considering (ring + two point size bodies) as a system.

${bf{Gamma }}_{cm}^{ext} = 0$ ; (torque of external forces about centre of mass of system equal to zero).

Therefore, the system’s angular momentum about the center of mass of system will remain constant.

${I_i}{{bf{omega }}_i} = {I_f}{{bf{omega }}_f}$

${I_{ring,,cm}}{{bf{omega }}_i} = ({I_{ring,,cm}} + {I_{bodies,,cm}}){{bf{omega }}_f}$

$Rightarrow quad M{R^2}{omega _i}hat k = M{R^2}{omega _f} + (m{R^2} + m{R^2}){{bf{omega }}_f}$

$Rightarrow quad frac{{M{R^2}{omega _i}hat k}}{{(M + 2m){R^2}}} = {{bf{omega }}_f}quad Rightarrow quad frac{{M{bf{omega }}}}{{M + 2m}} = {{bf{omega }}_f}$ .

Author

Rajesh Kumar

20 years of experience teaching high school and college physics to students across the globe.

When not teaching or mentoring, I write informative articles in physics and related subjects. So far, I have written more than 200 articles on different topics in physics. Apart from physics, I am proficient in engineering statics, dynamics, and calculus. I love spending time with my kids and listening to old Hindi songs.

Recent Posts

The Law of Conservation of Angular Momentum

Angular Momentum

Torque